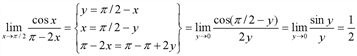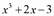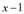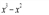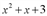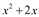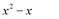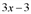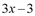1.2 Техника вычисления пределов

Используя определение предела, доказать, что 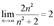, указать .

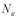Доказательство. Согласно определению предела числовой последовательности необходимо для любого 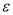 найти номер  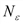такой, что при любых  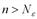выполнялось неравенство .

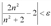Рассмотрим выражение под знаком модуля .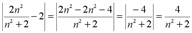

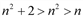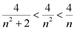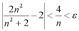Так как  можно записать цепочку неравенств . Так как нам не требуется найти наименьшее , можно записать , откуда  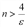и в этом случае  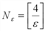— целая часть числа .

Итак, получается, что при 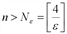 выполнено неравенство 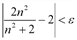,  что и требовалось доказать.

Доказать, что последовательность {xn}=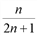 монотонная возрастающая.

Решение. Найдем член последовательности {xn+1}=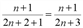 

Найдем знак разности: {xn}-{xn+1}= 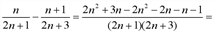 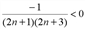, т.к. nN, то знаменатель положительный при любом n.

Таким образом, xn+1 > xn. Последовательность возрастающая, что и следовало доказать.

Выяснить является возрастающей или убывающей последовательность {xn} = .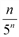

Решение. Найдем 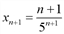. Найдем разность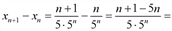 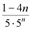, т.к.  nN, то 1 – 4n <0, т.е. хn+1 < xn. Последовательность монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Предел функции в точке х0.

Решение.

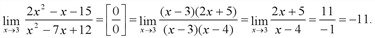
Для раскрытия неопределенности [0/0] раскладываем многочлены на множители. Выделяем в числителе и знаменателе сомножитель, который дает неопределенность. Для квадратного многочлена используется поиск корней через дискриминант. Для многочленов более высокого порядка используется прием деления многочлена на (х – х0).

Вычислить предел:

..

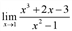Решение:

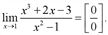
Для раскрытия неопределенности [0/0] разложим числитель и знаменатель дроби, стоящей под знаком предела, на множители. Заметим, что 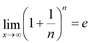.  Так как при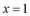 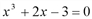 , значит,  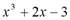делится на .

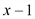Поделим «столбиком» многочлен x3 +2x-3 на двучлен x-1 :

Следовательно,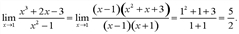 

Предел функции в бесконечности. Найти  .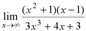

Решение.

Имеем неопределённость вида [∞/∞]. Для раскрытия неопределённости разделим почленно числитель и знаменатель на наивысшую степень х, т.е. на х3, предварительно раскрыв скобки.

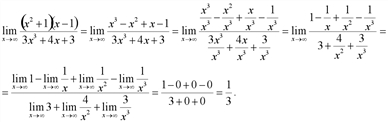При раскрытии неопределенности [∞/∞] предела отношения двух многочленов можно воспользоваться следующим правилом:

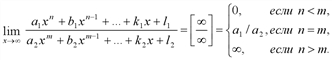
Например,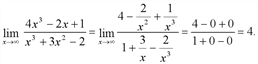 

Для раскрытия неопределенности [0/0] при нахождении предела функции умножаем числитель и знаменатель на сопряженное выражение, содержащее квадратный корень:

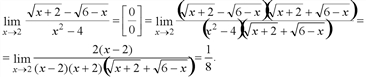
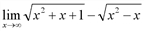
Решение. .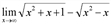

При 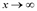 получаем в пределе 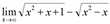неопределенность . Для вычисления данного предела домножим числитель и знаменатель дроби на сопряженное выражение 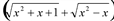, получим:

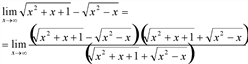
В числителе имеем разность квадратов:

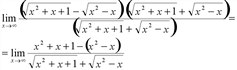
Раскрывая скобки в числителе и упрощая его, получим предел:

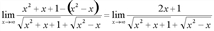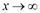. При  получаем неопределенность [∞/∞]. Для раскрытия неопределенности разделим выражения, стоящие в числителе и знаменателе, на высшую степень х (в числителе высшая степень – 1, в знаменателе тоже, поэтому делим на х в первой степени).

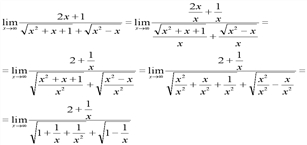
При 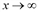 каждое из выражений  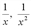стремится к нулю, поэтому числитель стремится к двум, а каждое подкоренное выражение знаменателя стремится к единице. Тогда предел в целом равен:

.

Ответ: 1.

Второй замечательный предел.

Выделяя целую часть у дроби, приводим выражение в скобках к виду второго замечательного предела :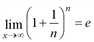

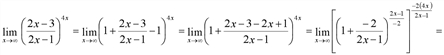
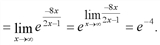
Вычислить предел числовой последовательности .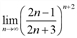

Решение:

Заметим, что 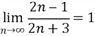, а 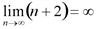, поэтому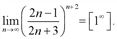 

Неопределенность вида 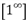 раскрывается с помощью второго замечательного предела .

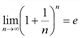Преобразуем выражение, стоящее под знаком предела следующим образом:

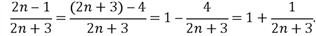
Итак,

Найти предел.

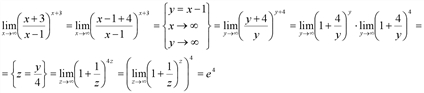
Вычислить предел функции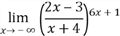 

Решение. Заметим, что 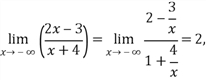 а 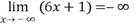    поэтому искомый предел равен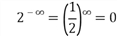, т. е. .

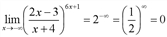Найти предел 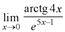 с помощью правила Лопиталя.

Решение. Под знаком предела числитель и знаменатель дроби стремятся к нулю при 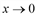, то приходим к неопределенности [0 / 0]. Выполняются все условия для применения правила Лопиталя. Применяя это правило имеем:

.

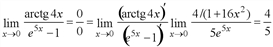Первый замечательный предел 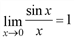 также может быть использован для нахождения предела функции: .

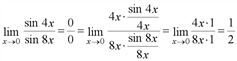▼ При стремлении аргумента 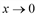можно использовать эквивалентные бесконечно малые величины:              

sin ax ~ ax, tg ax ~ ax, ex - 1 ~ x, ax – 1 ~ x ln a,

ln(1+x) ~ x, (1+x)m ~ 1+mx,

arcsin x ~ x, arctg x ~ x, 1-cos x ~ x2/2.

Найти предел.

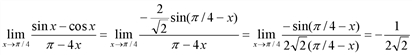
Найти предел.