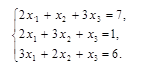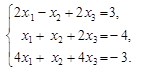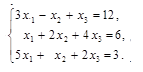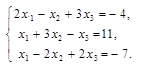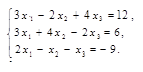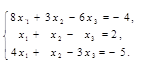1. По координатам точек А, В и С для указанных векторов найти:
- длину вектора
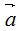 ;
; - скалярное произведение векторов
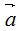 и
и 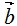 ; в)
; в) 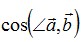 .
. - проекцию вектора
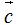 на вектор
на вектор 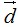 ;
; - координаты точки М, делящей отрезок р в отношении λ.
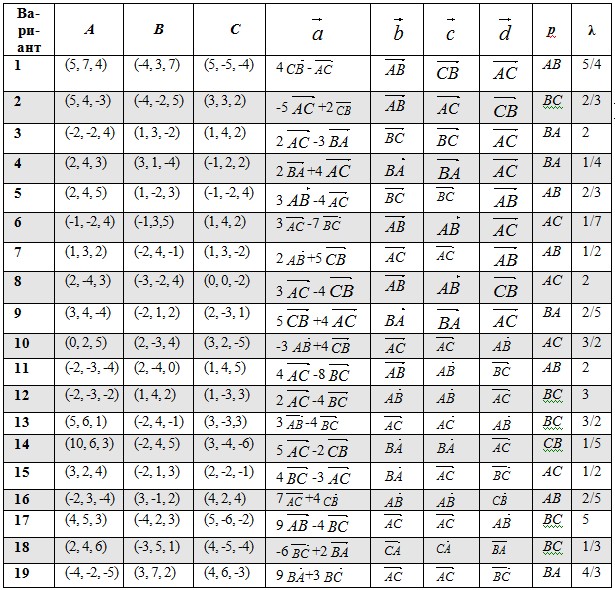
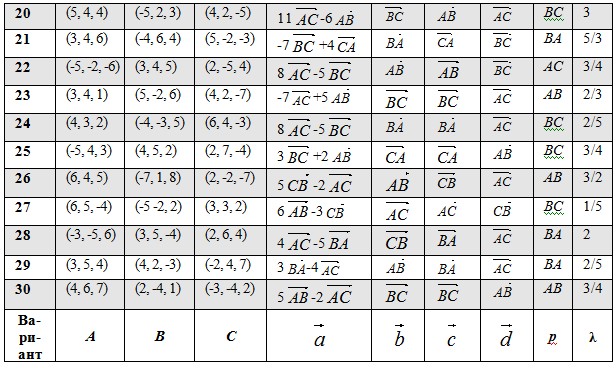
2. Разложить вектор 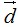 по векторам
по векторам 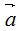 ,
, 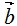 и
и 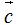 :
:
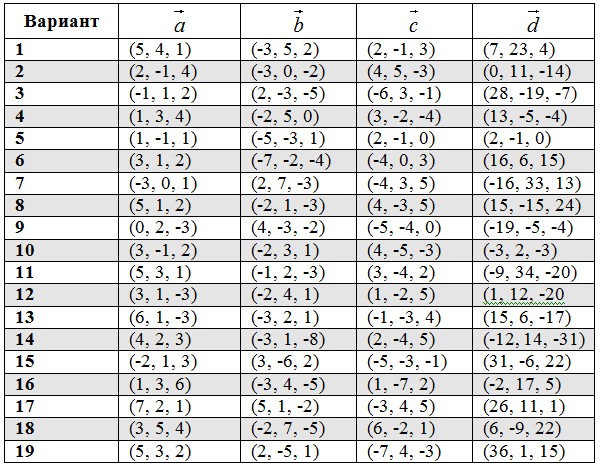
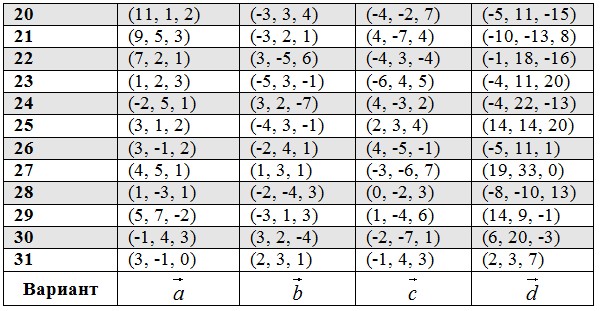
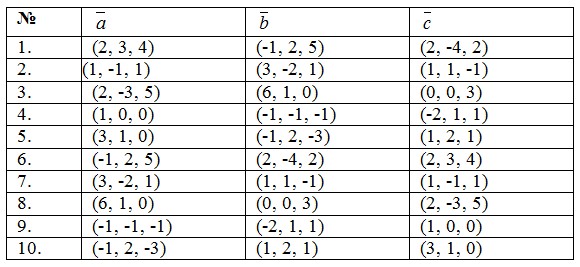
3. Даны векторы 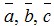 . Вычислить
. Вычислить 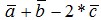 , угол между векторами
, угол между векторами 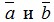 . Проверить, ортогональность векторов
. Проверить, ортогональность векторов 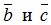
- Общее уравнение прямой линии и его варианты.
- Уравнение прямой, проходящей через точку по заданному направлению.
- Уравнение прямой, проходящей через две точки.
- Уравнение прямой в "отрезках".
- Угол между прямыми линиями. Параллельность и перпенди-кулярность прямых.
- Расстояние от точки до прямой.
- Взаимное расположение прямых на плоскости.
- Расстояние от точки до прямой. Пример.
- Уравнение плоскости в пространстве.
- Уравнение прямой в пространстве.
- Взаимное расположение прямой и плоскости в пространстве.
- Кривые второго порядка (окружность, эллипс, гипербола, парабола).
- Коллинеарные векторы. Компланарные векторы. Базис.
- Линейная зависимость векторов.
- Система координат. Ортонормированный базис.
- Скалярное произведение векторов.
- Векторное произведение векторов.
- Смешанное произведение векторов.
- Объем параллелепипеда, построенного на векторах.
- Определение вектора в n-мерном пространстве. Длина вектора.
- Разложение вектора по базису. Разложение вектора по ортам.
- Скалярное произведение векторов и его свойства.
- Множества точек. Геометрический смысл решения неравенств.
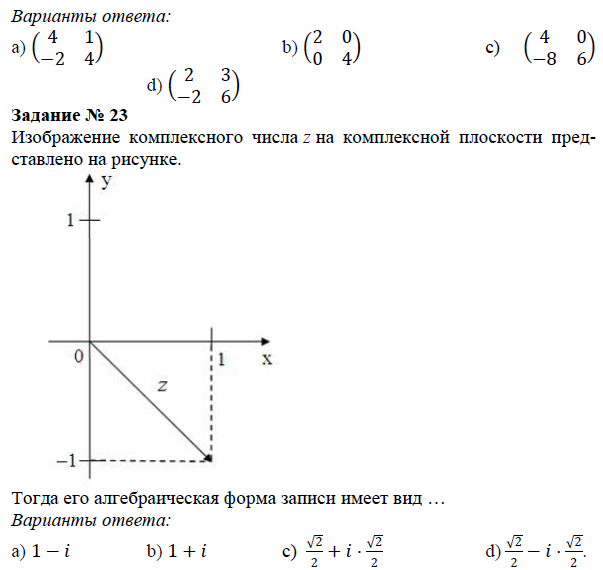
- Комплексные числа. Свойства комплексного числа. Опера-ции над комплексными числами.
- Тригонометрическая форма комплексного числа. Арифметические операции над комплексными числами в тригонометрической форме.
- Показательная форма комплексного числа. Возведение в степень и извлечение корня из комплексного числа.
1. Даны вершины треугольника А (7, 5), В (9, 4) и С (4, 5). Найти: а) уравнение стороны АВ; б) уравнение высоты СН; в) уравнение медианы АМ; г) точку N пересечения медианы АМ и высоты СН; д) уравнение прямой, проходящей через вершину С параллельно стороне АВ; е) расстояние от точки С до прямой АВ. Координаты точек А, В, С в таблице.
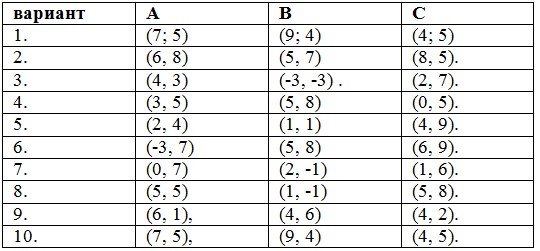
2. Найти мнимые и действительные части комплексных чисел:
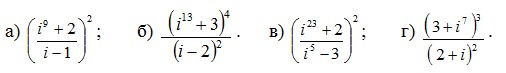
3. Найти модули и аргументы комплексных чисел:
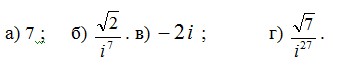
Задание №1. Треугольник АВС задан координатами вершин А, В, С.
AM – высота. ВN – медиана.
- написать уравнения сторон треугольника в трех эквивалентных формах;
- написать уравнение прямой L, проходящей через вершину В параллельно стороне АС;
- написать уравнения высоты АМ и медианы ВN;
- найти расстояние от вершины С до стороны АВ;
- найти координаты точки М.
–
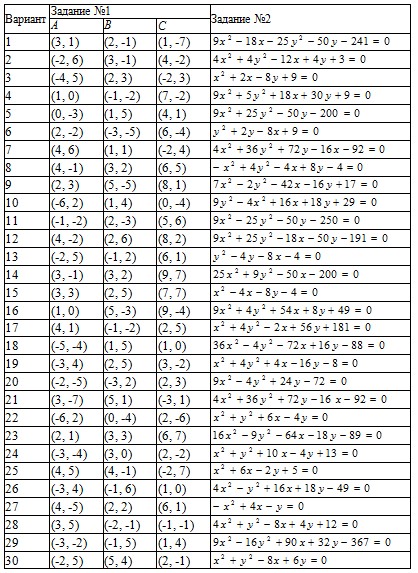
Задание №2. По общему уравнению кривой второго порядка определить тип кривой, начертить ее график, выписать основные параметры.
Номер варианта студента совпадает с его номером в списке учебной группы.
Содержание страницы
|
Вариант №1
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |
Вариант №2
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |
|
I семестр Вариант №3
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |
Вариант №4
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |
|
I семестр Вариант №5
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |
I семестр Вариант №6
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса. |