Пример 1. Решить систему линейных уравнений матричным методом:
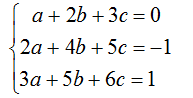
Решение: Введем обозначения:
А - матрица системы уравнений (состоит из коэффициентов при неизвестных);
Х - матрица-столбец, составленная из неизвестных;
В - матрица-столбец, составленная из свободных членов.
Тогда
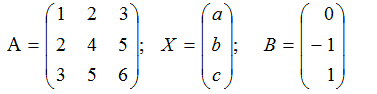
Запишем систему в матричной форме: АХ=В.
Решение системы будем находить по формуле:

где 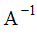 матрица, обратная матрице А.
матрица, обратная матрице А.
Найдем ее по формуле:
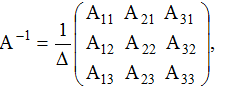
Где 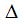 определитель матрицы
определитель матрицы 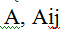 алгебраическое дополнение элемента
алгебраическое дополнение элемента 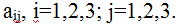
Вычислим алгебраические дополнения элементов первой строки:
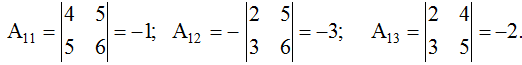
Тогда 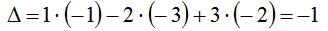 (вычислили определитель, предварительно разложив его по элементам первой строки).
(вычислили определитель, предварительно разложив его по элементам первой строки).
Остальные Вычислим алгебраические дополнения:
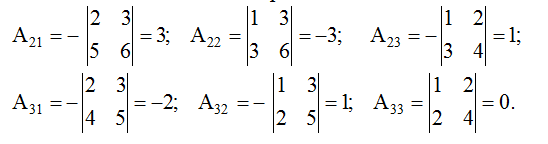
Тогда обратная матрица
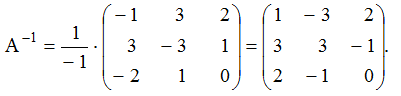
Воспользовавшись формулой (**) легко найти решение системы:
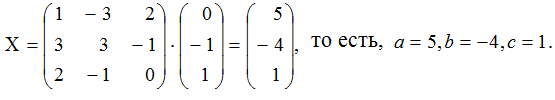
Пример 2. Решить методом Гаусса систему уравнений:

Решение: Метод Гаусса – это метод последовательного исключения переменных. Для решения системы данным методом исключим переменную из второго и третьего уравнения. Для этого умножим первое уравнение на 2 и вычтем из второго, затем умножим его на 3 и вычтем из третьего, при этом первое уравнение оставим без изменения. Получим систему:
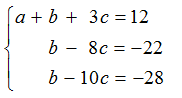
Далее второе уравнение оставим без изменения, а из третьего исключим переменную b. Далее второе уравнение системы оставим без изменения, а из третьего исключим переменную b. Получим следующую систему уравнений:
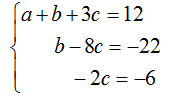
Осуществим «обратный ход» метода Гаусса. Из последнего уравнения получим:c=3 , из второго: b=2 и из первого: a=1, значит (1;2;3) – решение системы (*).(В этом можно убедиться проверкой: при непосредственной подстановке значений а, в и с в исходную систему получим верные равенства).
Ответ: (1;2;3).
Пример 3. Даны три последовательные вершины: А (-3; 0), В (2; 5), С (3; 2) параллелограмма ABCD для. Найти:
а) вершину D;
б) внутренний угол при вершине А;
в) уравнение высоты, проведенной из вершины А;
г) площадь параллелограмма.
Решение:
3а) Известно, что точка пересечения диагоналей делит диагонали пополам. Координаты середины отрезка равны полусуммам координат его концов. Найдем координаты точки F (точка пересечения диагоналей):
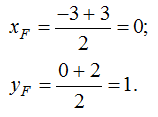
Тогда имеем F (0; 1). Точка D делит BF в отношении 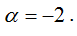 .
.
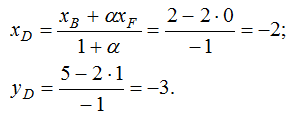
Тогда D(-2;-3)
3б) Угловой коэффициент прямой AD
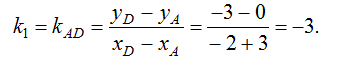
Угловой коэффициент прямой АВ
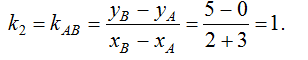
Угол 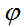 между прямыми находим по формуле:
между прямыми находим по формуле:
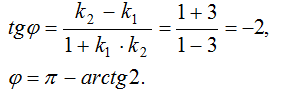
3в) АЕ – высота, проведенная из вершины А. Угловой коэффициент 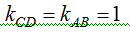 (по условию параллельности двух прямых), угловой коэффициент прямой АЕ
(по условию параллельности двух прямых), угловой коэффициент прямой АЕ
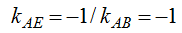 (по условию перпендикулярности двух прямых). Получим уравнение высоты АЕ по формуле уравнения прямой, проходящей через данную точку А (-3; 0) в данном направлении (k= - 1):
(по условию перпендикулярности двух прямых). Получим уравнение высоты АЕ по формуле уравнения прямой, проходящей через данную точку А (-3; 0) в данном направлении (k= - 1):
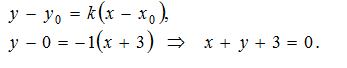
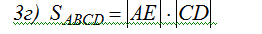
Найдем длину стороны СD:
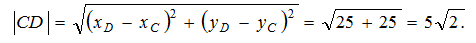
Определим длину высоты АЕ. Вспомним, что расстояние от точки 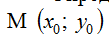 до прямой
до прямой 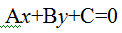 вычислим по формуле:
вычислим по формуле:
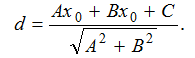
Вычислим расстояние от точки А (3; 0) до прямой СD (т.е. длину АЕ). Уравнение прямой АВ имеет вид:
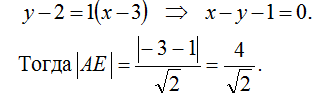
Найдем теперь площадь фигуры ABCD для:
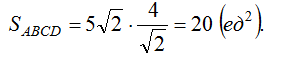
Пример 4. Решите систему уравнений при различных значениях параметра р:
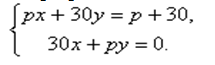
Решение. Система имеет единственное решение, если 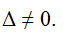
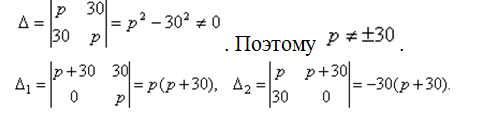
- При
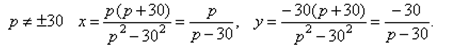
- При р p= 30 получаем систему уравнений
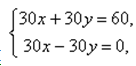 которая не имеет решений.
которая не имеет решений. - При р p= -30 система принимает вид
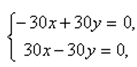 и, следовательно, имеет бесконечное множество решений
и, следовательно, имеет бесконечное множество решений 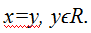
Пример 5. Определить знак квадратичной формы:
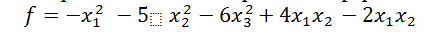
Составим матрицу для данной квадратичной формы:
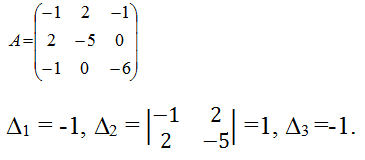
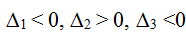
, по критерию Сильвестра f < 0 (отрицательно определена)
Пример 6. При каком значении параметра µ квадратичная форма будет положительно определена.
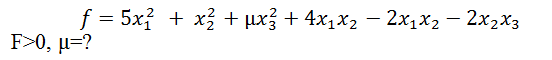
Матрица квадратичной формы:
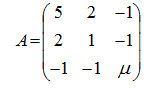
Проверим критерий Сильвестра:
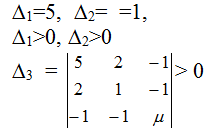
Вычислим данный определитель, раскладывая по элементам третьей строки.
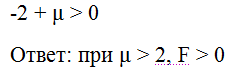
Написать комментарий
Ваше имя:Ваш комментарий:
Введите код, указанный на картинке:

