Множественная регрессия – регрессия между переменными 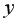 и
и 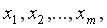 т.е. модель вида:
т.е. модель вида: 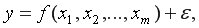
где 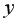 – зависимая переменная (результативный признак);
– зависимая переменная (результативный признак);
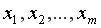 – независимые объясняющие переменные;
– независимые объясняющие переменные;
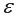 – возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов;
– возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов;
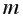 – число параметров при переменных
– число параметров при переменных 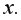
Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Уравнение множественной линейной регрессии в случае 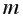 независимых переменных имеет вид
независимых переменных имеет вид 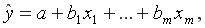 а в случае двух независимых переменных –
а в случае двух независимых переменных – 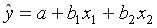 (двухфакторное уравнение).
(двухфакторное уравнение).
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов. Строится система нормальных уравнений:
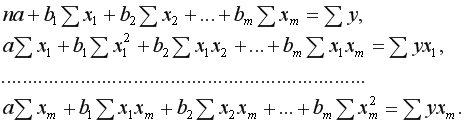
Решение этой системы позволяет получить оценки параметров регрессии с помощью метода определителей
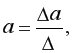
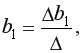 …,
…, 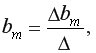
где 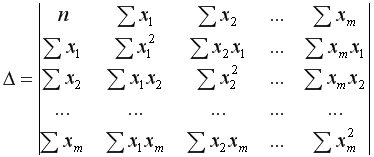 – определитель системы;
– определитель системы;
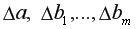 – частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными правой части системы.
– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными правой части системы.
Для двухфакторного уравнения коэффициенты множественной линейной регрессии можно вычислить по формулам:
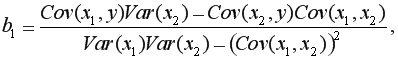
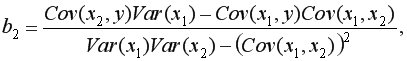
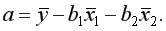
Частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии 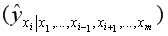 определять частные коэффициенты эластичности:
определять частные коэффициенты эластичности:
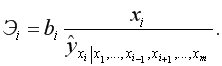
Средние коэффициентами эластичности показывают на сколько процентов в среднем изменится результат при изменении соответствующего фактора на 1%:
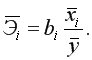
Их можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.
Тесноту совместного влияния факторов на результат оценивает коэффициент (индекс) множественной корреляции:
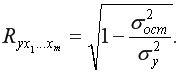
Величина индекса множественной корреляции лежит в пределах от 0 до 1 и должна быть больше или равна максимальному парному индексу корреляции: 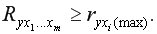
Чем ближе значение индекса множественной корреляции к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.
Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности (величина индекса множественной корреляции существенно отличается от индекса парной корреляции) включения в уравнение регрессии того или иного фактора.
При линейной зависимости совокупный коэффициент множественной корреляции определяется через матрицу парных коэффициентов корреляции:
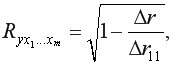
где 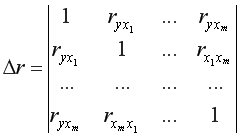 – определитель матрицы парных коэффициентов корреляции;
– определитель матрицы парных коэффициентов корреляции;
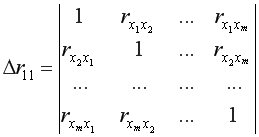 – определитель матрицы межфакторной корреляции.
– определитель матрицы межфакторной корреляции.
Частные коэффициенты корреляциихарактеризуют тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Если вычисляется, например, 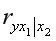 (частный коэффициент корреляции между
(частный коэффициент корреляции между 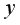 и
и 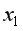 при фиксированном влиянии
при фиксированном влиянии 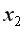 ), это означает, что определяется количественная мера линейной зависимости между
), это означает, что определяется количественная мера линейной зависимости между 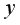 и
и 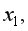 которая будет иметь место, если устранить влияние на эти признаки фактора
которая будет иметь место, если устранить влияние на эти признаки фактора 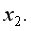
Частные коэффициенты корреляции, измеряющие влияние на 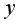 фактора
фактора 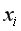 при неизменном уровне других факторов, можно определить как:
при неизменном уровне других факторов, можно определить как:
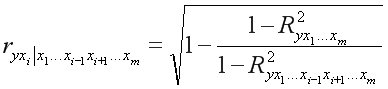
или по рекуррентной формуле:
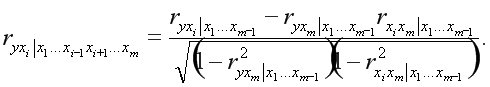
Для двухфакторного уравнения:
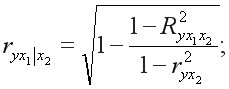
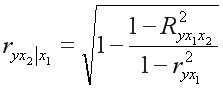 или
или
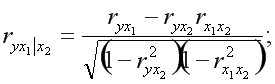
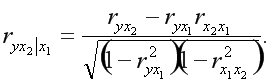
Частные коэффициенты корреляции изменяются в пределах от -1 до +1.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции 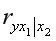 получится меньше, чем соответствующий парныйкоэффициент
получится меньше, чем соответствующий парныйкоэффициент 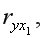 значит взаимосвязь признаков
значит взаимосвязь признаков 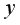 и
и 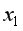 в некоторой степени обусловлена воздействием на них фиксируемой переменной
в некоторой степени обусловлена воздействием на них фиксируемой переменной 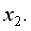 И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная
И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная 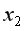 ослабляет своим воздействием связь
ослабляет своим воздействием связь 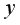 и
и 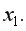
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, 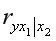 – коэффициент частной корреляции первого порядка.
– коэффициент частной корреляции первого порядка.
Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент множественной корреляции:
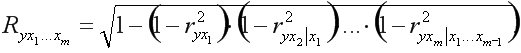
Качество построенной модели в целом оценивает коэффициент (индекс) множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции: 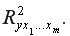 Индекс множественной детерминации фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как
Индекс множественной детерминации фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как 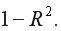
Если число параметров при 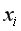 близко к объему наблюдений, то коэффициент множественной корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможногопреувеличения тесноты связи, используется скорректированный индекс множественной корреляции, который содержит поправку на число степеней свободы:
близко к объему наблюдений, то коэффициент множественной корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможногопреувеличения тесноты связи, используется скорректированный индекс множественной корреляции, который содержит поправку на число степеней свободы:
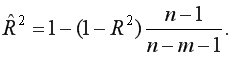
Чем больше величина 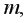 тем сильнее различия
тем сильнее различия 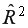 и
и 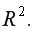
Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным 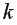 =
=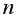 -
-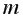 -2.
-2.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 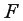 -критерия Фишера:
-критерия Фишера:
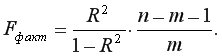
Мерой для оценки включения фактора в модель служит частный 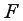 -критерий. В общем виде для фактора
-критерий. В общем виде для фактора 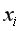 частный
частный 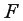 -критерий определяется как
-критерий определяется как
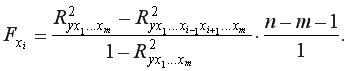
Для двухфакторного уравнения частные 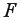 -критерии имеют вид:
-критерии имеют вид:
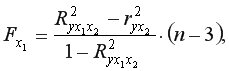
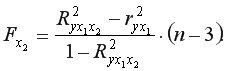
Если фактическое значение 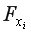 превышает табличное, то дополнительное включение фактора
превышает табличное, то дополнительное включение фактора 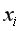 в модель статистически оправданно и коэффициент чистой регрессии
в модель статистически оправданно и коэффициент чистой регрессии 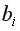 при факторе
при факторе 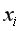 статистически значим. Если же фактическое значение
статистически значим. Если же фактическое значение 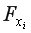 меньше табличного, то фактор
меньше табличного, то фактор 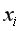 нецелесообразно включать в модель, а коэффициент регрессии при данном факторе в этом случае статистически незначим.
нецелесообразно включать в модель, а коэффициент регрессии при данном факторе в этом случае статистически незначим.
Для оценки значимости коэффициентов чистой регрессии по 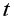 -критерию Стьюдента используется формула:
-критерию Стьюдента используется формула:
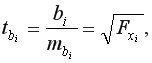
где 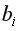 – коэффициент чистой регрессии при факторе
– коэффициент чистой регрессии при факторе 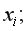
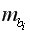 – средняя квадратическая (стандартная) ошибка коэффициента регрессии
– средняя квадратическая (стандартная) ошибка коэффициента регрессии 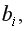 которая может быть определена по формуле:
которая может быть определена по формуле:
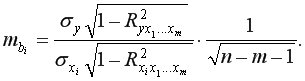
При дополнительном включении в регрессию нового фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если это не так, то включаемый в анализ новый фактор не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по 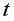 -критерию Стьюдента.
-критерию Стьюдента.
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 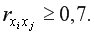 Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель, тем меньше мультиколлинеарность факторов.
Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора 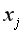 остатки
остатки 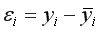 имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. При нарушении гомоскедастичности выполняются неравенства
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. При нарушении гомоскедастичности выполняются неравенства 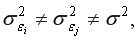
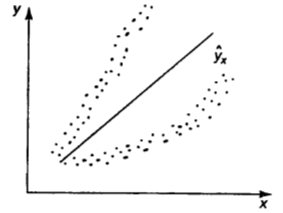
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 9.22).
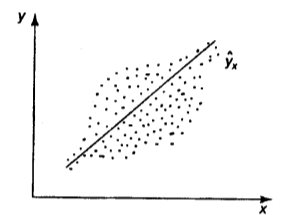
а)б)
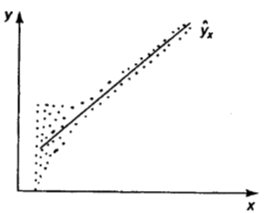
в)
Рис. 9.22. Примеры гетероскедастичности:
а) дисперсия остатков растет по мере увеличения 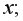
б) дисперсия остатков достигает максимальной величины при средних значениях переменной 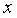 и уменьшается при минимальных и максимальных значениях
и уменьшается при минимальных и максимальных значениях 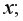
в) максимальная дисперсия остатков при малых значениях 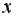 и дисперсия остатков однородна по мере увеличения значений
и дисперсия остатков однородна по мере увеличения значений 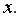
Для проверки выборки на гетероскедастичность можно использовать метод Гольдфельда-Квандта (при малом объеме выборки) или критерий Бартлетта (при большом объеме выборки).
Последовательность применения теста Гольдфельда-Квандта:
1) Упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2) Исключить из рассмотрения 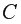 центральных наблюдений. При этом
центральных наблюдений. При этом 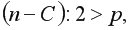 где
где 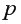 – число оцениваемых параметров. Из экспериментальных расчетов для случая однофакторного уравнения регрессии рекомендовано при
– число оцениваемых параметров. Из экспериментальных расчетов для случая однофакторного уравнения регрессии рекомендовано при 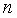 =30 принимать
=30 принимать 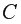 =8, а при
=8, а при 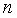 =60 соответственно
=60 соответственно 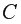 =16.
=16.
3) Разделить совокупность из 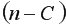 наблюдений на две группы (соответственно с малыми и большими значениями фактора
наблюдений на две группы (соответственно с малыми и большими значениями фактора 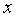 ) и определить по каждой из групп уравнение регрессии.
) и определить по каждой из групп уравнение регрессии.
4) Вычислить остаточную сумму квадратов для первой 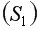 и второй
и второй 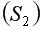 групп и найти их отношение
групп и найти их отношение 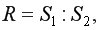 где
где 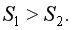 При выполнении нулевой гипотезы о гомоскедастичности отношение
При выполнении нулевой гипотезы о гомоскедастичности отношение 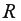 будет удовлетворять
будет удовлетворять 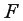 -критерию Фишера со степенями свободы
-критерию Фишера со степенями свободы 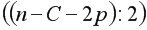 для каждой остаточной суммы квадратов. Чем больше величина
для каждой остаточной суммы квадратов. Чем больше величина 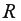 превышает
превышает 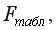 тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Если необходимо включить в модель факторы, имеющие два или более качественных уровней (пол, профессия, образование, климатические условия, принадлежность к определенному региону и т.д.), то им должны быть присвоены цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные называют фиктивными (искусственными) переменными.
Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. Значимость влияния фиктивной переменной проверяется с помощью 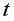 -критерия Стьюдента.
-критерия Стьюдента.
Написать комментарий
Ваше имя:Ваш комментарий:
Введите код, указанный на картинке:


 (тыс. ден. ед.) от объема произведенной продукции
(тыс. ден. ед.) от объема произведенной продукции 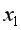 (тыс. ед.) и расходов на сырье
(тыс. ед.) и расходов на сырье 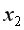 (тыс. ден. ед). Необходимо:
(тыс. ден. ед). Необходимо: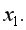
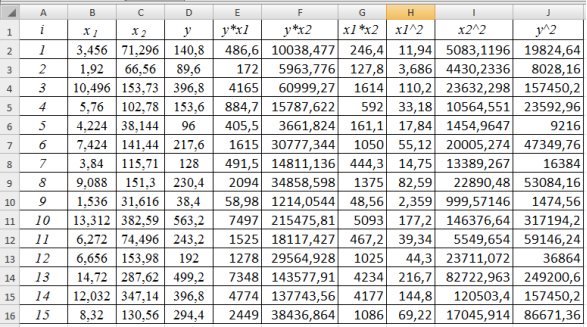
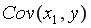 =345,5;
=345,5; 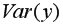 =13838,89;
=13838,89; 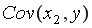 =8515,78;
=8515,78; 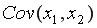 =219,315;
=219,315; 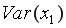 =9,37;
=9,37; 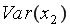 =6558,08.
=6558,08.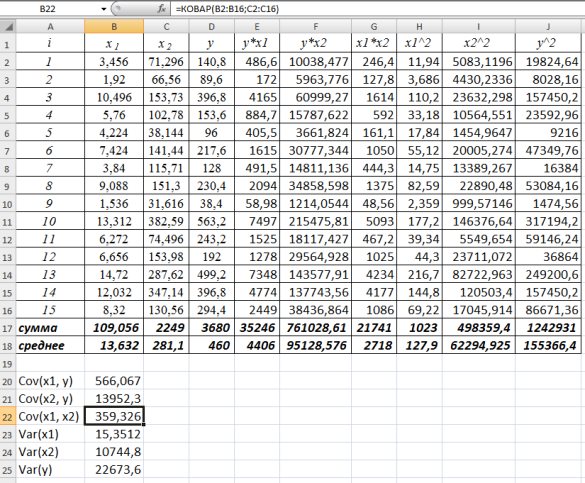
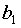 используем формулы
используем формулы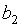 =0,301 и Коэффициент
=0,301 и Коэффициент 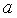 =-31,25 (рис. 9.25.).
=-31,25 (рис. 9.25.).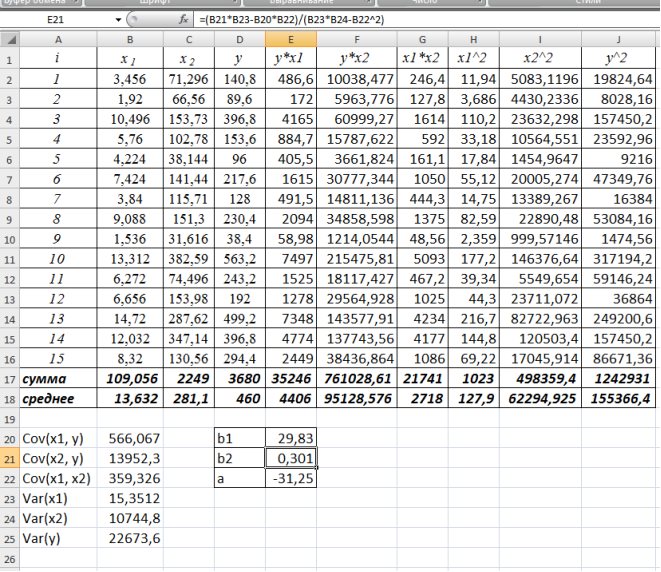
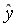 =-31,25+29,83
=-31,25+29,83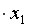 +0,301
+0,301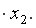
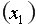 на 1 тыс. ед. затраты на выпуск этой продукции
на 1 тыс. ед. затраты на выпуск этой продукции 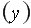 в среднем увеличатся на 29,83 тыс. ден. ед., а при увеличении расходов на сырье
в среднем увеличатся на 29,83 тыс. ден. ед., а при увеличении расходов на сырье 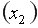 на 1 тыс. ден. ед. затраты увеличатся в среднем на 0,301 тыс. ден. ед.
на 1 тыс. ден. ед. затраты увеличатся в среднем на 0,301 тыс. ден. ед.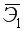 =0,884 и
=0,884 и 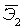 =0,184. Т.е. увеличение только объема произведенной продукции (от своего среднего значения) или только расходов на сырье на 1% увеличивает в среднем затраты на выпуск продукции на 0,884% или 0,184% соответственно. Таким образом, фактор
=0,184. Т.е. увеличение только объема произведенной продукции (от своего среднего значения) или только расходов на сырье на 1% увеличивает в среднем затраты на выпуск продукции на 0,884% или 0,184% соответственно. Таким образом, фактор 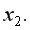
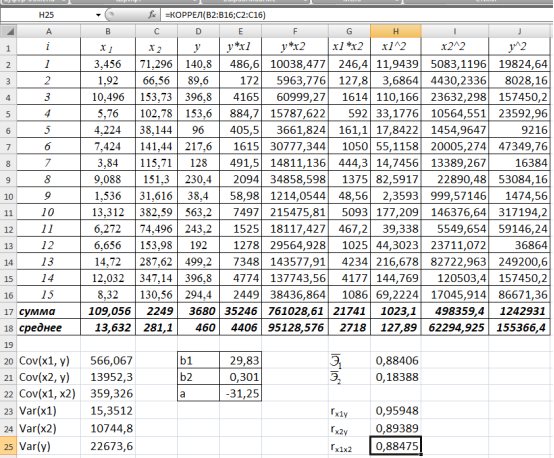
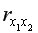 очень сильная (
очень сильная (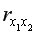 =0,88>0,7), что говорит о том, что один из факторов является неинформативным, т.е. в модель необходимо включать или
=0,88>0,7), что говорит о том, что один из факторов является неинформативным, т.е. в модель необходимо включать или 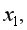 или
или 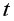 -критерия Стьюдента.
-критерия Стьюдента. 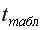 =2,1604 определяем с помощью встроенной статистической функции СТЬЮДРАСПОБР взяв
=2,1604 определяем с помощью встроенной статистической функции СТЬЮДРАСПОБР взяв 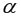 =0,05 и
=0,05 и 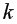 =
=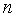 -2=13.
-2=13.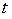 -критерия Стьюдента для каждого парного коэффициента определим по формулам:
-критерия Стьюдента для каждого парного коэффициента определим по формулам: 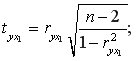
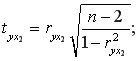
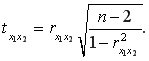 . Результат расчета представлен на рис. 9.27.
. Результат расчета представлен на рис. 9.27.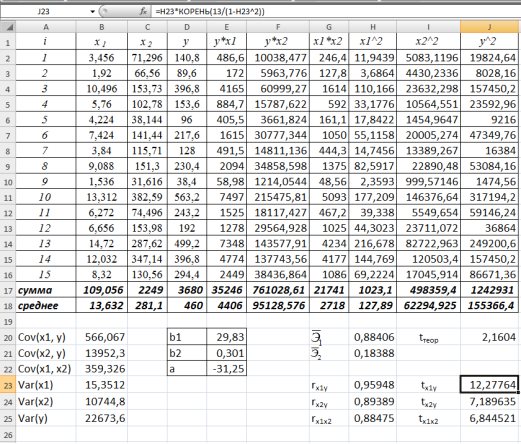
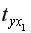 =12,278;
=12,278; 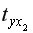 =7,1896;
=7,1896; 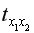 =6,845.
=6,845.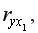
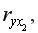
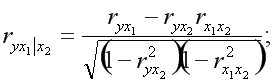
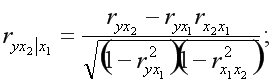
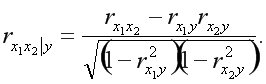
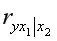 =0,81;
=0,81; 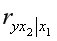 =0,34;
=0,34; 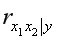 =0,21. Таким образом, фактор
=0,21. Таким образом, фактор 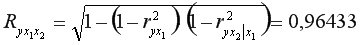 .
.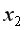 характеризуется как очень тесная, в которой
характеризуется как очень тесная, в которой 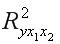 =93% вариации затрат на выпуск продукции определяются вариацией учтенных в модели факторов: объема произведенной продукции и расходов на сырье. Прочие факторы, не включенные в модель, составляют соответственно 7% от общей вариации
=93% вариации затрат на выпуск продукции определяются вариацией учтенных в модели факторов: объема произведенной продукции и расходов на сырье. Прочие факторы, не включенные в модель, составляют соответственно 7% от общей вариации 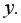
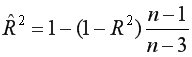 =0,9182 указывает на тесную связь между результатом и признаками.
=0,9182 указывает на тесную связь между результатом и признаками.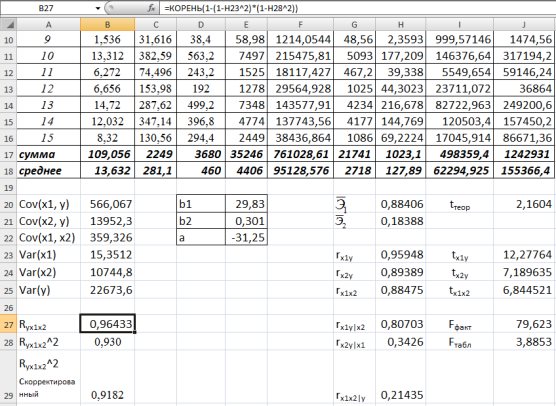
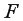 -критерия Фишера. Вычислим
-критерия Фишера. Вычислим 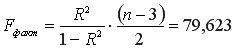 .
. 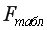 =3,8853 определяем взяв
=3,8853 определяем взяв 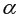 =0,05,
=0,05, 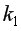 =2,
=2, 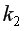 =15-2-1=12 помощью встроенной статистической функции FРАСПОБР с такими же параметрами.
=15-2-1=12 помощью встроенной статистической функции FРАСПОБР с такими же параметрами.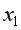 с помощью частного
с помощью частного 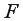 -критерия Фишера по формулам
-критерия Фишера по формулам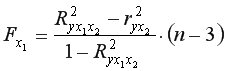 ;
; 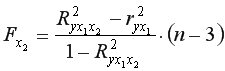 .
.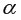 =0,05,
=0,05, 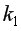 =1,
=1, 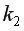 =12 «=FРАСПОБР(0,05;1;12)», результат –
=12 «=FРАСПОБР(0,05;1;12)», результат – 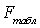 =4,747. Так как
=4,747. Так как 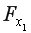 =22,4127>
=22,4127>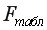 =4,747, а
=4,747, а 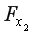 =1,5958<
=1,5958<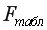 =4,747, то включение фактора
=4,747, то включение фактора 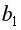 статистически значим, а дополнительное включение фактора
статистически значим, а дополнительное включение фактора 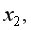 после того, как уже введен фактор
после того, как уже введен фактор 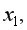 нецелесообразно (рис. 9.29).
нецелесообразно (рис. 9.29).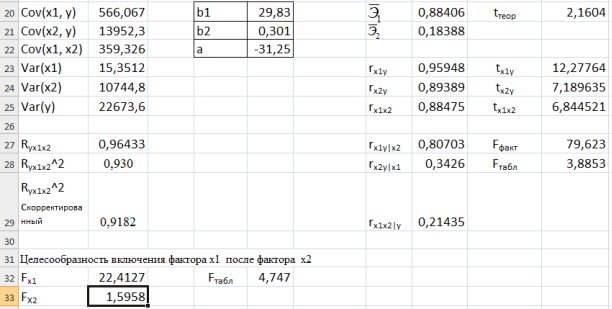
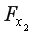 (немногим больше 1) свидетельствует о статистической незначимости прироста
(немногим больше 1) свидетельствует о статистической незначимости прироста 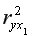 за счет включения в модель фактора
за счет включения в модель фактора 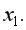 Это означает, что парная регрессионная модель зависимости затрат на выпуск продукции от объема произведенной продукции является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор
Это означает, что парная регрессионная модель зависимости затрат на выпуск продукции от объема произведенной продукции является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор 
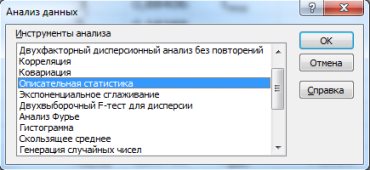
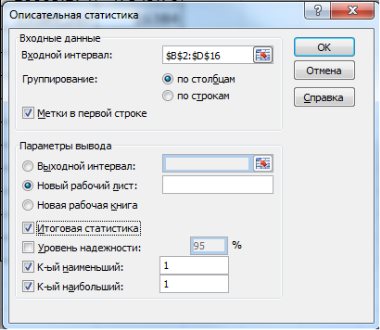
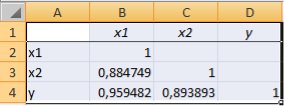
 -го наибольшего и наименьшего значений нужно установить соответствующие флажки в диалоговом окне.
-го наибольшего и наименьшего значений нужно установить соответствующие флажки в диалоговом окне.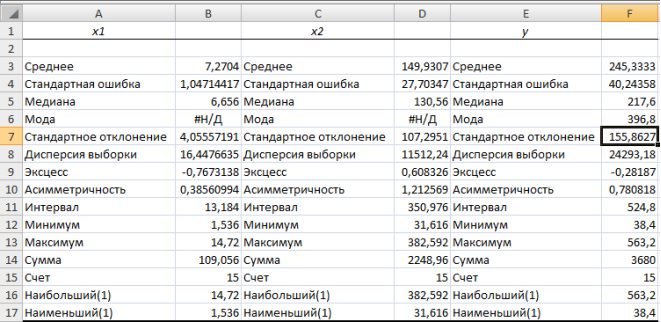
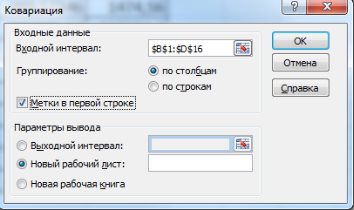
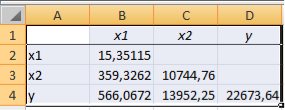
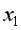 и
и 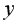 – 566,0672; между
– 566,0672; между 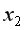 и
и 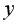 – 13952,25. Выборочная дисперсия
– 13952,25. Выборочная дисперсия 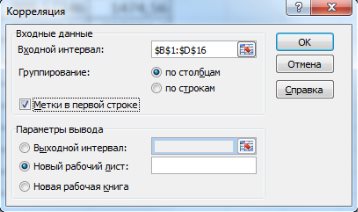
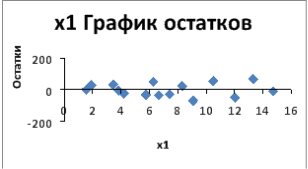
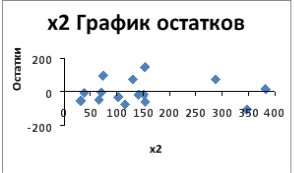
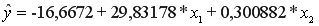
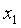 и
и 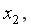 видим, что расположение остатков не имеет направленности. Следовательно, они независимы от значений
видим, что расположение остатков не имеет направленности. Следовательно, они независимы от значений 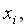 значит построенная модель адекватна.
значит построенная модель адекватна.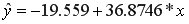 ; вычислены теоретические значения
; вычислены теоретические значения 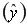 и остатки
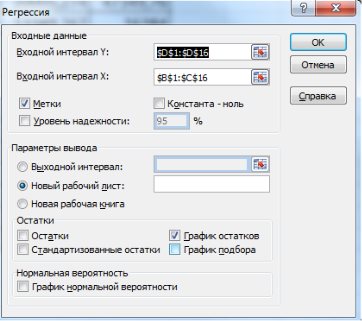
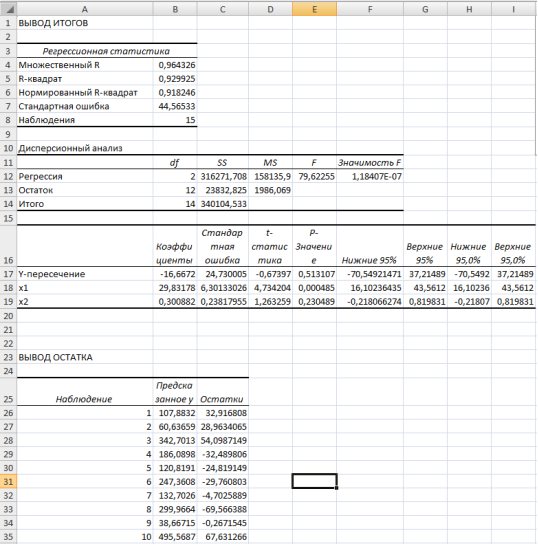
и остатки  Эти результаты можно получить намного проще, используя регрессионный анализ. Для этого в диалоговом окне ввода параметров инструмента Регрессия нужно поставить флажок напротив «Остатки» и в Excel дополнительно будет выведены сведения, как на рис. 9.39.
Эти результаты можно получить намного проще, используя регрессионный анализ. Для этого в диалоговом окне ввода параметров инструмента Регрессия нужно поставить флажок напротив «Остатки» и в Excel дополнительно будет выведены сведения, как на рис. 9.39.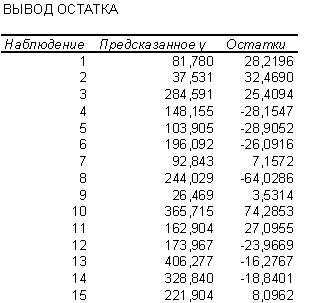
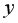 – это теоретические значения
– это теоретические значения 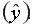
 а использовать результаты регрессионного анализа.
а использовать результаты регрессионного анализа.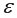 не обнаруживают тенденцию по мере увеличения
не обнаруживают тенденцию по мере увеличения 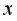 и
и 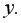 Следовательно, есть равенство дисперсий остаточных величин, т.е. не наблюдается гетероскедастичности остатков.
Следовательно, есть равенство дисперсий остаточных величин, т.е. не наблюдается гетероскедастичности остатков.
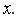 Исключим из рассмотрения
Исключим из рассмотрения 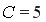 центральных наблюдений. Разделим оставшуюся совокупность из 15-5=10 наблюдений на две группы (по 5) и определим по каждой из групп уравнение регрессии (рис. 9.41).
центральных наблюдений. Разделим оставшуюся совокупность из 15-5=10 наблюдений на две группы (по 5) и определим по каждой из групп уравнение регрессии (рис. 9.41).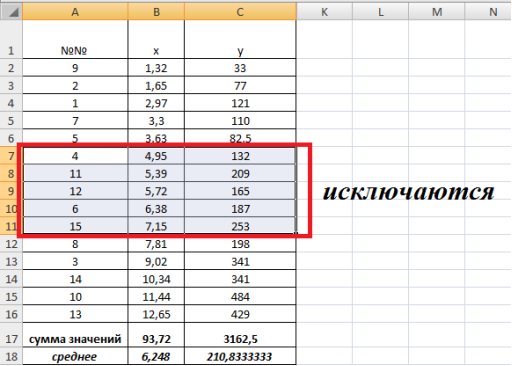
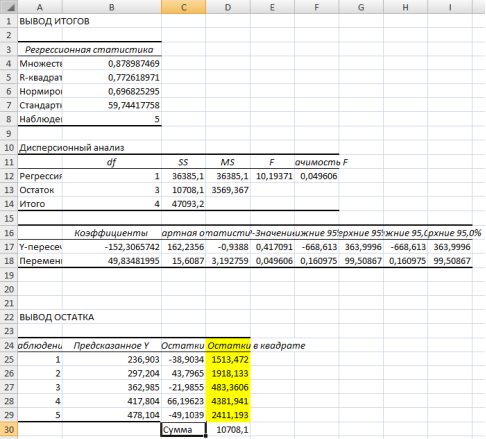
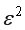 и суммы по каждой группе.
и суммы по каждой группе.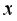
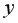
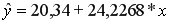
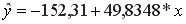
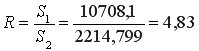
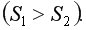
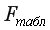 =9,28 при 5%-ном уровне значимости и числе степеней свободы
=9,28 при 5%-ном уровне значимости и числе степеней свободы 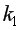 =
=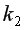 =(15-5-2·2):2=3.
=(15-5-2·2):2=3.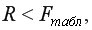 то гетероскедастичность остатков отсутствует.
то гетероскедастичность остатков отсутствует.