Максимизация прибыли.
Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Перечислим лишь некоторые: предельные издержки, предельный доход, предельная производительность, предельная полезность, предельная склонность к потреблению и т.д. Все эти величины самым тесным образом связаны с понятием производной. В качестве характерного примера рассмотрим предельные издержки.
Пусть q – количество произведенной продукции, С(q) – соответствующие данному выпуску издержки. Предельные издержки обозначаются МС и определяются как дополнительные издержки, связанные с производством дополнительной единицы продукции. Другими словами, MC = C∙(q + ∆q) – C(q),где ∆q = 1. Используя равенство ∆С = dC, получим, MC = ∆C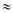 dC = C'(q) ∙ ∆q = C'(q).
dC = C'(q) ∙ ∆q = C'(q).
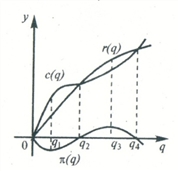
Рис. 6.
Таким образом, данное выше определение МС, по существу, не противоречит другому распространенному определению, согласно которому МС = С'.
Рассмотрим экономическую интерпретацию теоремы Ферма. Пусть С=С(q)- функция издержек, r=r(q) – функция дохода, 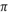 =
=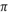 (x) – функция прибыли. Тогда
(x) – функция прибыли. Тогда 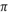 (q)=r(q)-C(q). Оптимальным уровнем производства, очевидно, является такой, при котором прибыль максимальна, т.е. такое значение выпуска
(q)=r(q)-C(q). Оптимальным уровнем производства, очевидно, является такой, при котором прибыль максимальна, т.е. такое значение выпуска 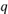 , при котором функция прибыли
, при котором функция прибыли 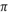 (q) имеет максимум. В силу теоремы Ферма в этой точке q =
(q) имеет максимум. В силу теоремы Ферма в этой точке q = 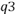 производная равна нулю:
производная равна нулю: 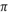 ’(
’(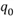 )=0. Но
)=0. Но 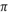 ’(q)=D’(q)-S’(q), поэтому
’(q)=D’(q)-S’(q), поэтому
D’(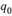 )=S’(
)=S’(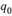 ). (*)
). (*)
Производная C’(q) выражает предельные издержки MC, а производственная r’(q) – предельный подход Mr. Таким образом, равенство (*), полученное с помощью теоремы Ферма, приобретая вид MC (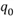 ) = Mr (
) = Mr (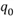 ).
).
Последнее равенство есть выражение одного из базовых законов микроэкономики: максимум прибыли достигается при равенстве предельных издержек и предельного дохода.
Оптимизация налогообложения.
Пусть t – налог с единицы выпускаемой продукции, C=C(q)- функция издержек, r=r(q) – функция дохода, 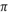 =
=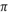 (q) – функция прибыли. Тогда функция прибыли имеет вид:
(q) – функция прибыли. Тогда функция прибыли имеет вид: 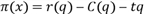 .
.
Пусть, например, цена на продукцию 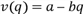 , т.е. линейно уменьшается с увеличением объема продукции, а функция издержек имеет вид
, т.е. линейно уменьшается с увеличением объема продукции, а функция издержек имеет вид 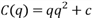 .
.
Здесь a,b,c, - некоторые положительные константы. Функция прибыли в этом случае имеет вид
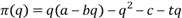 .
.
Желая максимизировать прибыль, фирма ищет оптимальный объем производства. Условие максимума прибыли: 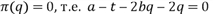 , откуда
, откуда 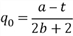 .
.
При таком значении объема продукции суммарный налог T имеет вид 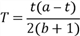 . Интересы государства заключаются в том, чтобы величина T была максимальной. Дифференцируем T и, приравнивая производную к нулю:
. Интересы государства заключаются в том, чтобы величина T была максимальной. Дифференцируем T и, приравнивая производную к нулю: 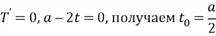 .
.
Рассмотрим эту задачу при конкретных числовых значениях констант a,b,и с.Пусть a=80, b=1, c=10. Тогда 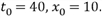 При этих значениях максимальная величина прибыли
При этих значениях максимальная величина прибыли 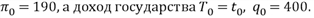 (Заметим, что при отсутствии налогов максимальная прибыль достигалась бы при вдвое большем объеме производства
(Заметим, что при отсутствии налогов максимальная прибыль достигалась бы при вдвое большем объеме производства 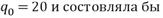
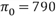 )
)
Функции двух переменных в экономике.
Рассмотрим еще раз максимизацию прибыли.
Пусть F(K,L)-производственная функция (где K и L – соответственно затраты капитала и трудовых ресурсов), P- цена продукции. Функция прибыли П вычисляется обычно по формуле
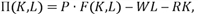
Где W и R – соответственно цены на труд и капитальные затраты, W и R – положительные числа.
Точка (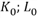 ) называется оптимальным планом, если в ней функция прибыли принимает максимальное значение.
) называется оптимальным планом, если в ней функция прибыли принимает максимальное значение.
Рассмотрим задачу: найти предельную норму замещения производственной функции F
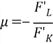
При оптимальном плане.
В точке локального максимума первые частные производные функции прибыли П(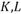 ) равны нулю. Система в данном случае имеет вид
) равны нулю. Система в данном случае имеет вид
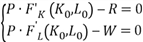
Отсюда 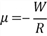 .
.
Рассмотрим теперь задачу максимизации функции прибыли.
Написать комментарий
Ваше имя:Ваш комментарий:
Введите код, указанный на картинке:


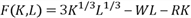 .
.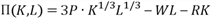 .
.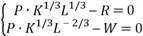
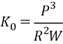 ,
, 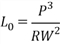
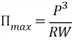
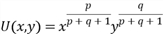 и потребитель стремиться максимизировать функцию полезности.
и потребитель стремиться максимизировать функцию полезности.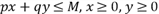
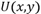 . Вычислим частные производные функции полезности:
. Вычислим частные производные функции полезности: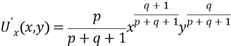 ;
;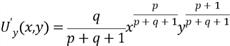 ;
;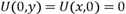 , поэтому надо искать точку максимума на прямой
, поэтому надо искать точку максимума на прямой 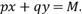
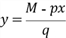 (**)
(**)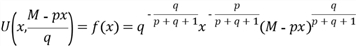 .
.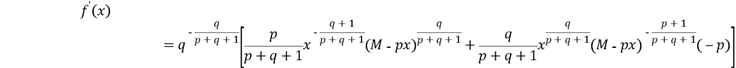 .
.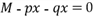 , откуда
, откуда 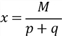 и с учетом (**)
и с учетом (**) 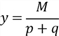 .
.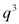 . Тогда дополнительные издержки, связанные с увеличением выпуска от q до q + 1, составят ∆С = C∙(q + 1) – C(q), что приближенно равно С'(q) = 1500 ‑ 44q + 0,006q2.
. Тогда дополнительные издержки, связанные с увеличением выпуска от q до q + 1, составят ∆С = C∙(q + 1) – C(q), что приближенно равно С'(q) = 1500 ‑ 44q + 0,006q2.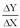 . Приращение ∆X в различных случаях задается по-разному. В одних случаях ∆X - это наиболее естественная единица измерения величины X, в других случаях ∆X – это разность между соседними значениями в таблице, задающей функцию Y от X. В теоретических вопросах, однако, более удобным является определение MY, основанное на равенстве MY=
. Приращение ∆X в различных случаях задается по-разному. В одних случаях ∆X - это наиболее естественная единица измерения величины X, в других случаях ∆X – это разность между соседними значениями в таблице, задающей функцию Y от X. В теоретических вопросах, однако, более удобным является определение MY, основанное на равенстве MY=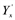 . Конечно, при таком определении приходится дополнительно предполагать, что является дифференцируемой функцией от X.
. Конечно, при таком определении приходится дополнительно предполагать, что является дифференцируемой функцией от X.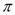 (q) = R(q) – C(q).
(q) = R(q) – C(q).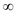 ) и дифференцируемы при q > 0.
) и дифференцируемы при q > 0.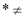 0.
0.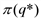 положителен
положителен 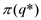 > 0), условие q
> 0), условие q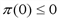 (нет выпуска – нет выручки, нет выручки – нет прибыли).
(нет выпуска – нет выручки, нет выручки – нет прибыли).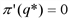 . Так как
. Так как 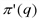 = R'(q) –C'(q) то в точке q = q* получаем равенство: R'(q*) =C’(q*)
= R'(q) –C'(q) то в точке q = q* получаем равенство: R'(q*) =C’(q*)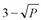 . Эффективная область «работы» этой формулы от 1 до 9 руб. При какой цене за порцию мороженного совокупная выручка будет максимальной?
. Эффективная область «работы» этой формулы от 1 до 9 руб. При какой цене за порцию мороженного совокупная выручка будет максимальной?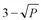 )∙P. Требуется найти наибольшее значение этой функции на отрезке[1; 9]. Для этого находим критические точки этой функции, принадлежащие данному отрезку:
)∙P. Требуется найти наибольшее значение этой функции на отрезке[1; 9]. Для этого находим критические точки этой функции, принадлежащие данному отрезку: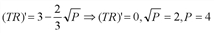
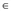 [0;
[0; 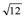 ]. Так как
]. Так как 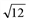 ] в некоторой точке q* на этом отрезке она принимает наибольшее значение. Поскольку
] в некоторой точке q* на этом отрезке она принимает наибольшее значение. Поскольку 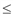 0 при q >
0 при q > 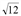 , то
, то 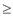 0. Получим 15 = С'(q*) = 3(q*)2 + 3, откуда q*= 2. Так как фирма стремится получить максимальную прибыль, то она будет производить 2 единицы продукции.
0. Получим 15 = С'(q*) = 3(q*)2 + 3, откуда q*= 2. Так как фирма стремится получить максимальную прибыль, то она будет производить 2 единицы продукции.
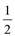 q2 – издержки фирмы-монополиста, QD (p) = 40 – 2p – функция спроса. Найти зависимость цены р от количества произведенной продукции q.
q2 – издержки фирмы-монополиста, QD (p) = 40 – 2p – функция спроса. Найти зависимость цены р от количества произведенной продукции q.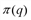 имеет вид
имеет вид 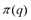 = (20 –
= (20 – 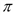 '(q*) = 20 – 2q* = 0. Находим оптимальный (для монополии) объем производства q* = 10.
'(q*) = 20 – 2q* = 0. Находим оптимальный (для монополии) объем производства q* = 10.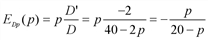 , поэтому
, поэтому 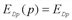 (15) = –3. Следовательно,
(15) = –3. Следовательно, 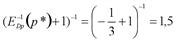 .
.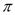 (0) = С(0) = 5 денежных единиц. Очевидно, что убыточное производство возможно только на коротком интервале времени, поэтому найденная функция предложения является функцией предложения в краткосрочном периоде.
(0) = С(0) = 5 денежных единиц. Очевидно, что убыточное производство возможно только на коротком интервале времени, поэтому найденная функция предложения является функцией предложения в краткосрочном периоде.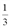 ∙q3 – 2q2 + 9q + 20.
∙q3 – 2q2 + 9q + 20.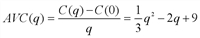 .
.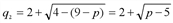 . Неравенство C'(q)> AVC(q) эквивалентно следующим неравенствам:
. Неравенство C'(q)> AVC(q) эквивалентно следующим неравенствам: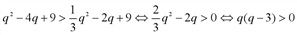
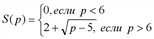 .
.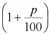 раз, т. е. Q1=Q0
раз, т. е. Q1=Q0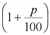 , Q2=Q0
, Q2=Q0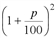 , … Qt=Q0
, … Qt=Q0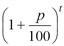 .
.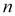 раз, то при том же ежегодном приросте р % процент начисления за
раз, то при том же ежегодном приросте р % процент начисления за 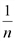 -ю часть года составит
-ю часть года составит 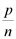 %, а размер вклада за t при nt начислениях составит Qt=Q0
%, а размер вклада за t при nt начислениях составит Qt=Q0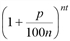 .
.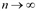 ), тогда размер вклада за t лет составит:
), тогда размер вклада за t лет составит: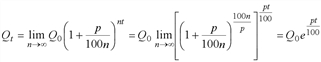 .
.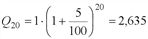 ден. ед.;
ден. ед.;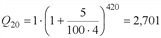 ден. ед;
ден. ед; 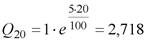 ден. ед.
ден. ед.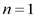 ), при одной и той же процентной ставке (p=5 %) оказалась незначительной (около 2,5 %).
), при одной и той же процентной ставке (p=5 %) оказалась незначительной (около 2,5 %).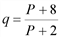 и предложение
и предложение 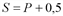 , где
, где 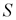 и
и 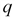 количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, 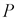 – цена товара.
– цена товара.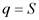 или
или 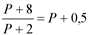 . Откуда
. Откуда 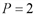 , т.е. равновесная цена равна 2 ден. ед.
, т.е. равновесная цена равна 2 ден. ед.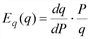 и
и 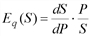 .
.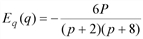 и
и 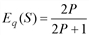 .
.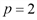 имеем
имеем 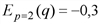 и
и 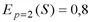 .
.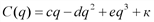 и
и 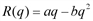 , где
, где 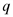 - объем производства;
- объем производства; 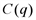 - издержки;
- издержки; 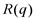 - доход,
- доход, 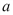 ,
, 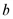 ,
, 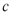 ,
,  , ,к,
, ,к, 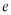 - параметры.
- параметры.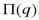 от объема производства.
от объема производства.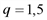 ед.
ед.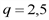 ед.
ед.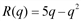 ,
, 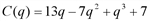 .
.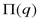 от объема производства:
от объема производства: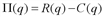 ,
,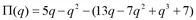 ,
,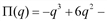 7
7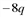 .
.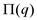 и построим ее график (рис. 1). Функция
и построим ее график (рис. 1). Функция 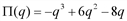 определена и непрерывна на всей числовой прямой. Однако из условия задачи следует, что
определена и непрерывна на всей числовой прямой. Однако из условия задачи следует, что 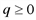 , поэтому исследуем функцию только для
, поэтому исследуем функцию только для 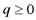 , т.е. в интервале
, т.е. в интервале 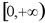 . Находим точки пересечения с осью
. Находим точки пересечения с осью 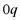 :
: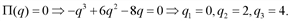 График функции проходит через точки (0;0), (2;0), (4;0). Исследуем функцию с помощью производных. Имеем:
График функции проходит через точки (0;0), (2;0), (4;0). Исследуем функцию с помощью производных. Имеем: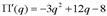 ,
, 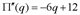 . Найдем критические точки:
. Найдем критические точки: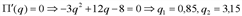 ;
; 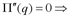
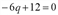
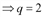 .
.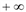 )
)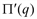
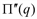
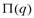
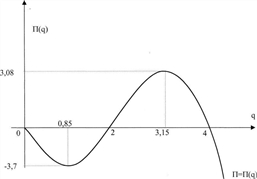
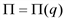 асимптот не имеет. По полученным данным строим кривую (рис. 2).
асимптот не имеет. По полученным данным строим кривую (рис. 2).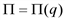 (см. выше) показывает, что прибыль равна 0 при объемах производства
(см. выше) показывает, что прибыль равна 0 при объемах производства 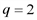 и
и 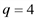 (точки пересечения графика с осью
(точки пересечения графика с осью 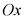 ).
).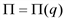 с осью 0q, прибыль максимальна при q=3,15 (точка максимума функции
с осью 0q, прибыль максимальна при q=3,15 (точка максимума функции 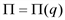 ), убытки максимальны при q=0,85 (точка минимума функции
), убытки максимальны при q=0,85 (точка минимума функции 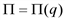 ).
).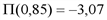 ,
, 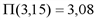 .
.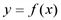 равно
равно 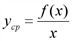 , получим соответственно средние значения прибыли в расчете на единицу объема производства:
, получим соответственно средние значения прибыли в расчете на единицу объема производства: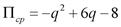 .
.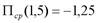 .
.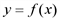 равно
равно 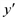 , то предельные значения прибыли равно:
, то предельные значения прибыли равно: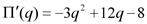 .
.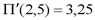 .
.
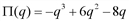
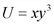 , где х и у – некоторые блага.
, где х и у – некоторые блага.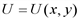 (скалярная функция) растет быстрее всего в направлении
(скалярная функция) растет быстрее всего в направлении 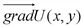 . Найдем частные производные
. Найдем частные производные 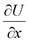 и
и 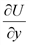 в точке (2;1):
в точке (2;1):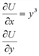
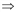
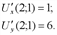
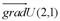 имеет координаты 1 и 6, т.е.
имеет координаты 1 и 6, т.е. 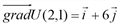 . Следовательно, функция
. Следовательно, функция 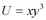 в точке (2;1) растет быстрее всего в направлении вектора
в точке (2;1) растет быстрее всего в направлении вектора 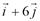 .
.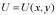 в точке (2;1) равна модулю
в точке (2;1) равна модулю 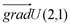 , т.е.
, т.е. 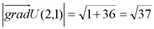 .
.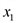 и
и 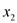 ,
, 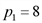 и
и 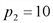 - цены на эти товары,
- цены на эти товары, 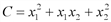 - функция затрат. Найти план производства, при котором функция прибыли максимальна.
- функция затрат. Найти план производства, при котором функция прибыли максимальна.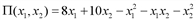 .
.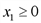 ,
, 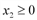 .
.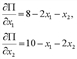

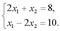
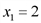 ,
, 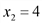 .
.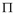 , для чего найдем:
, для чего найдем: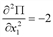 ;
; 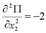 ;
; 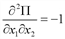 .
.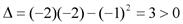 , то точка (2;4) есть точка экстремума, а учитывая, что
, то точка (2;4) есть точка экстремума, а учитывая, что 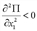 , заключим, что это и точка максимума. Следовательно, максимальная прибыль
, заключим, что это и точка максимума. Следовательно, максимальная прибыль 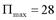 достигается при плане производства
достигается при плане производства 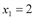 и
и 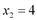 .
.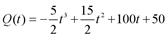 (ед), где t – рабочее время, ч. Вычислить производительность труда, скорость и темп ее изменения через час после начала рабочего дня и за час до его окончания.
(ед), где t – рабочее время, ч. Вычислить производительность труда, скорость и темп ее изменения через час после начала рабочего дня и за час до его окончания.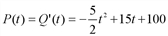 (ед./ч), а скорость и темп изменение производительности – соответственно производной P'(t) и логарифмической производной
(ед./ч), а скорость и темп изменение производительности – соответственно производной P'(t) и логарифмической производной 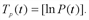 Имеем P'(t) = -5t + 15 (ед/ч
Имеем P'(t) = -5t + 15 (ед/ч ).
).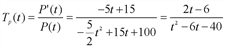 (1/ч).
(1/ч).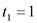 и
и 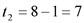 соответственно имеем:
соответственно имеем: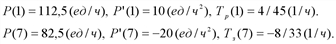
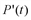 и
и 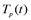 с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется ее снижением в последние часы
с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется ее снижением в последние часы