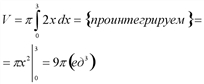Площадь криволинейной трапеции, ограниченной кривой y = f(x) и вертикальными прямыми x = a и x = b, находится по формуле
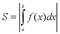 .
.
Объем тела, полученного вращением вокруг оси Ох кривой y = f(x), ограниченной справа и слева прямыми x = a и x = b, может быть найден по следующей формуле:
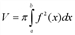
Пример.
Вычислить площадь фигуры, ограниченной линиями 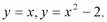
Решение. Найдем точки пересечения заданных линий, решив систему этих уравнений. Получим А(-1,0), B(2,2). На отрезке 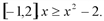 Тогда
Тогда
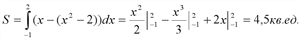
Примеры.
Определить сходимость интегралов.
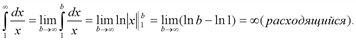
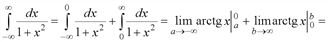
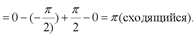
Вычислить площадь криволинейной трапеции, ограниченной линиями y = x, y = x2, x = 2.[2]
Решение.
а) вычислить площади криволинейной трапеции, ограниченной линиями y = x, y = x2, x = 2.
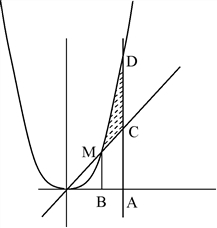
Построим чертеж:
|
Очевидно, что площадь криволинейной трапеции CDM(заштрихована на рисунке) может быть найдена как разность площадей двух фигур: ADMB и ACMB. Фигура ADMBограничена кривой у = х2 и прямыми у = 0, х = 2, х = 1(уравнение последней прямой следует из точки М– точки пересечения параболы у = х2 и прямой у = х). Ее площадь равна: |
Фигура ACMB ограничена прямыми у = 0, у = х, х = 2, х = 1 и ее площадь равна: 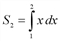 .В итоге получаем:
.В итоге получаем:
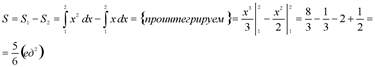
Ответ: 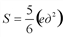
Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной параболой у2 = 2х, прямой х = 3 и осью Ох.
Построим вспомогательный чертеж.
|
|
Криволинейная трапеция CDMограничена кривой у2 = 2х и прямыми у = 0, х = 0, х = 3. В этом случае объем тела вращения равен:
Теперь вычислим определенный интеграл:
|
Ответ: 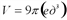 .
.
Написать комментарий
Ваше имя:Ваш комментарий:
Введите код, указанный на картинке:


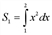
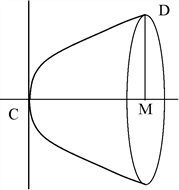
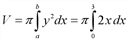 .
.