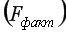Часть I. Модель парной регрессии

Парная регрессия – регрессия (связь) между двумя переменными и 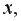 т.е. модель вида: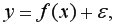 

где  – зависимая переменная (результативный признак);

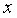 – независимая объясняющая переменная (признак-фактор);

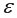– возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов.

Практически в каждом отдельном случае величина  складывается из двух слагаемых: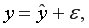 

где 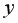 – фактическое значение результативного признака;

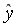 – теоретическое значение результативного признака, найденное исходя из уравнения регрессии. Знак «^» означает, что между переменным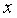и  и  нет строгой функциональной зависимости.

Различают линейные и нелинейные регрессии.

Линейная регрессия описывается уравнением прямой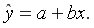 

Нелинейные регрессии делятся на два класса:

1) регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам, например:

• полиномы разных степеней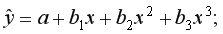 

• равносторонняя гипербола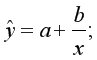 

2) регрессии, нелинейные по оцениваемым параметрам, например:

• степенная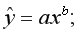 

• показательная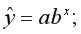 

• экспоненциальная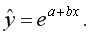 

Для построения парной линейной регрессии вычисляют вспомогательные величины (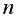 – число наблюдений).

Выборочные средние: 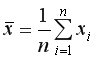 и 

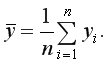
Выборочная ковариация между 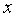 и 

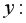
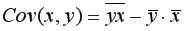 или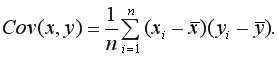 

Ковариация – это числовая характеристика совместного распределения двух случайных величин.

Выборочная дисперсия для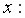 

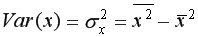 или 

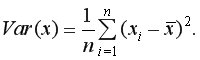
Выборочная дисперсия для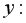 

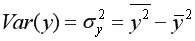 или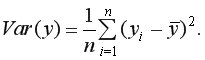 

Выборочная дисперсияхарактеризует степень разброса значений случайной величины вокруг среднего значения (вариабельность, изменчивость).

Тесноту связи изучаемых явлений оценивает выборочный коэффициент корреляции между 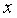 и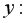 

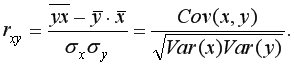
Коэффициент корреляции изменяется в пределах от -1 до +1. Чем ближе от по модулю к 1, тем ближе статистическая зависимость между 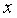 и  к линейной функциональной.

Если 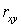=0, то линейная связь между  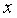и  отсутствует; 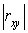<0,3 – связь слабая; 0,3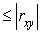<0,7 – связь умеренная; 0,7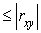<0,9 – связь сильная; 0,9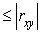<0,99 – связь весьма сильная.

Положительное значение коэффициента свидетельствует о том, то связь между признаками прямая (с ростом 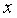 увеличивается значение ), отрицательное значение – связь обратная (с ростом 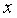 значение  уменьшается).

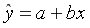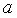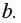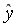Построение линейной регрессии  сводится к оценке ее параметров  и  Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака  от теоретических  минимальна, т.е.

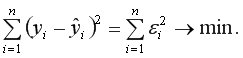
Для линейной регрессии параметры 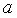 и 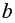 находятся из системы нормальных уравнений:

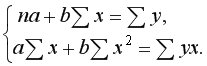
Решая систему, находим выборочный коэффициент линейной регрессии  на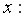 

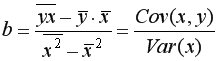
и параметр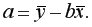 

Коэффициент 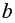 при факторной переменной 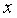показывает, насколько изменится в среднем величина при изменении фактора 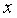на единицу измерения.

Параметр 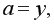 когда 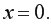 Если 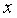 не может быть равен 0, то  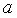не имеет экономического смысла. Интерпретировать можно только знак пр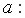и  если 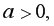 то относительное изменение результата происходит медленнее, чем изменение фактора, т.е. вариация результата меньше вариации фактора и наоборот.

Для оценки качества построенной модели регрессии можно использовать коэффициент детерминации либо среднюю ошибку аппроксимации.

Коэффициент детерминации

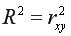 или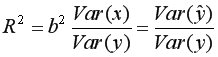 

показывает долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака 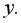 Соответственно, величина  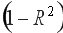характеризует долю дисперсии показателя  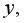вызванную влиянием неучтенных в модели факторов и прочих причин.

Чем ближе 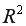 к 1, тем качественнее регрессионная модель, т.е. построенная модель хорошо аппроксимирует исходные данные.

Средняя ошибка аппроксимации – это среднее относительное отклонение теоретических значений 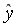 от фактических  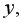т.е.

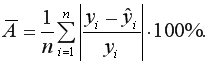
Построенное уравнение регрессии считается удовлетворительным, если значение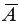не превышает 10-12%.

Для линейной регрессии средний коэффициент эластичности находится по формуле:

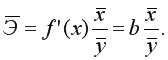
Средний коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится результат  от своей величины при изменении фактора 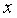 на 1% от своего значения.

Оценка значимости уравнения регрессии в целом дается с помощью 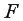-критерия Фишера, который заключается в проверке гипотезы о статистической незначимости уравнения регрессии. Для этого выполняется сравнениефактического  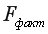и критического (табличного)  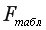значений 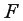-критерия Фишера.

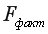определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы, т.е.

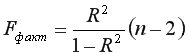
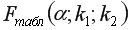– максимально возможное значение критерия под влиянием случайных факторов при степенях свободы 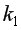=1, 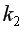=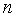-2 и уровне значимости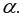 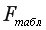  находится из таблицы 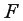-критерия Фишера (таблица 1 приложения).

Уровень значимости 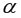 – это вероятность отвергнуть правильную гипотезу при условии, что она верна.

Если 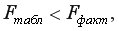 то гипотеза об отсутствии связи изучаемого показателя с фактором отклоняется и делается вывод о существенности этой связи с уровнем значимости  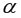(т.е. уравнение регрессии значимо).

Если 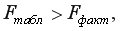 то гипотеза принимается и признается статистическая незначимость и ненадежность уравнения регрессии.

Для линейной регрессии значимость коэффициентов регрессии оценивают с помощью 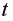-критерия Стьюдента, согласно которому выдвигается гипотеза о случайной природе показателей, т.е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия  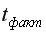для каждого из оцениваемых коэффициентов регрессии, т.е.

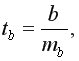
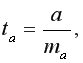
где 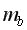 и 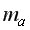 – стандартные ошибки параметров линейной регрессии определяются по формулам:

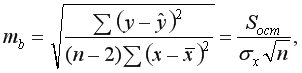
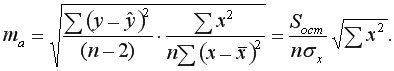
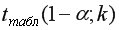 – максимально возможное значение критерия Стьюдента под влиянием случайных факторов при данной степени свободы 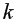=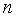-2 и уровне значимости  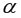находится из таблицы критерия Стьюдента (таблица 2 приложения).

Если 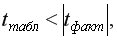 то гипотеза о несущественности коэффициента регрессии отклоняется с уровнем значимости  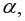т.е. коэффициент ( 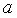или 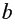)не случайно отличается от нуля и сформировался под влиянием систематически действующего фактора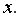 

Если 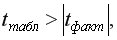 то гипотеза не отклоняется и признается случайная природа формирования параметра.

Значимость линейного коэффициента корреляции также проверяется с помощью 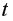-критерия Стьюдента, т.е.

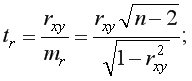
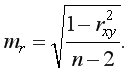
Гипотеза о несущественности коэффициента корреляции отклоняется с уровнем значимост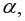и  если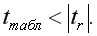 

Замечание.Для линейной парной регрессии проверки гипотез о значимости коэффициента 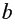 и коэффициента корреляции  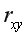равносильны проверке гипотезы о существенности уравнения регрессии в целом, т.е.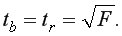 

Для расчета доверительного интервала определяют предельную ошибку для каждого показателя, т.е.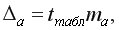  

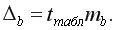
Доверительные интервалы для коэффициентов линейной регрессии:

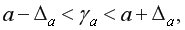
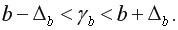
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, т.к. он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение 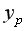 определяется путем подстановки в уравнение регрессии  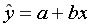соответствующего прогнозного значения  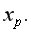Затем вычисляется средняя стандартная ошибка прогноза

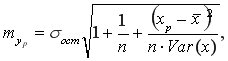где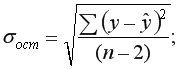 

и строится доверительный интервал прогноза

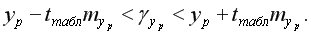
Интервал может быть достаточно широк за счет малого объема наблюдений.

Регрессии, нелинейные по включенным переменным, приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью МНК.

Гиперболическая регрессия: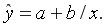 

Линеаризующее преобразование: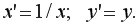 

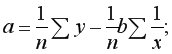
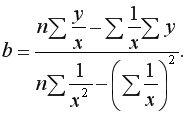
Регрессии,нелинейные по оцениваемым параметрам, делятся на два типа: внутренне нелинейные 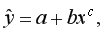 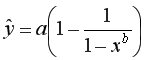 и т.п. (к линейному виду не приводятся) и внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований), например:

Экспоненциальная регрессия: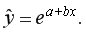 

Линеаризующее преобразование: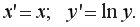 

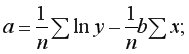
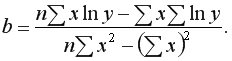
Степенная регрессия: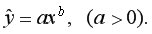 

Линеаризующее преобразование: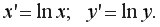 

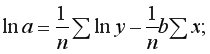
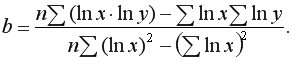
Показательная регрессия: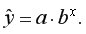 

Линеаризующее преобразование: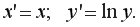 

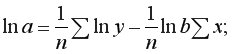
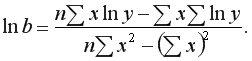
Логарифмическая регрессия: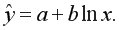 

Линеаризующее преобразование: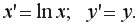 

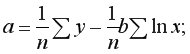
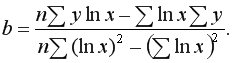
Пример 9.1. По 15 сельскохозяйственным предприятиям (табл. 9.1) известны:  – количество техники на единицу посевной площади (ед/га) и  – объем выращенной продукции (тыс. ден. ед.). Необходимо:

1) определить зависимость  от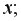 

2) построить корреляционные поля и график уравнения линейной регрессии на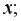 

3) сделать вывод о качестве модели и рассчитать прогнозное значение 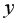 при прогнозном значении  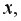составляющем 112% от среднего уровня.

Таблица 9.1

Решение:

1) В Excel составим вспомогательную таблицу 9.2.

Таблица 9.2

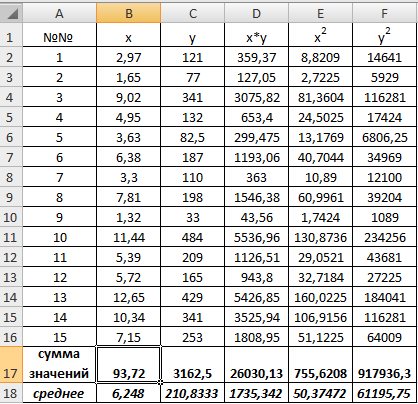
Рис. 9.1. Таблица для расчета промежуточных значений

Вычислим количество измерений 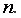 Для этого в ячейку В19 поместим =СЧЁТ(A2:A16).

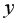С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех  (ячейка В17) и (ячейка С17).

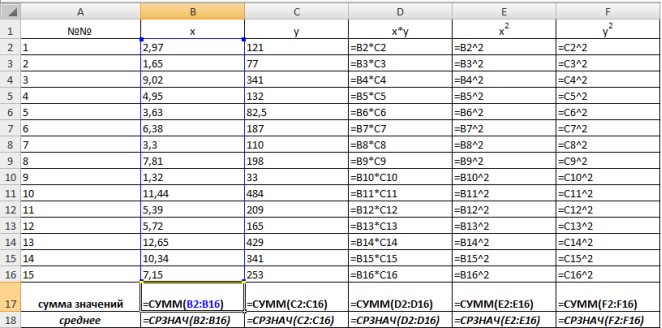
Рис. 9.2. Расчет суммы значений и средних

Для вычисления средних значений используем встроенную функцию MS Excel СРЗНАЧ(), в скобках указывается диапазон значений для определения средней. Таким образом, средний объем выращенной продукции по 15 хозяйствамсоставляет 210,833 тыс.ден. ед., а средние количество техники – 6,248ед/га.

Для заполнения столбцов D, E, Fвведем формулувычисления произведения: в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.

Для вычисления выборочной ковариациимежду 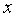 и 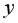 используем формулу  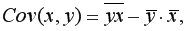т.е. в ячейку B21 поместим =D18-B18*C18 и получим 418,055 (рис. 9.3).

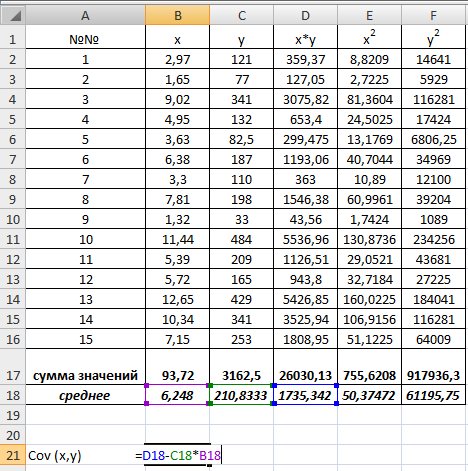
Рис. 9.3. Вычисление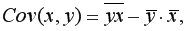 

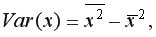Выборочную дисперсиюдля  найдем по формуле  для этого в ячейку B22 поместим =E18-B18^2 (^- знак указывающий возведение в степень) и получим 11,337. Аналогично определяем 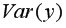=16745,05556 (рис. 9.4)

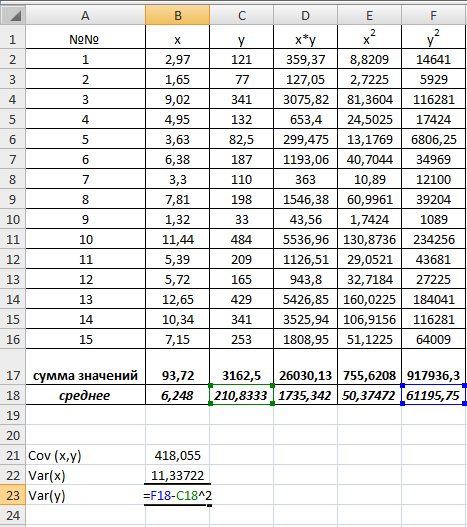
Рис. 9.4. Вычисление Var(x) и Var (y)

Далее используя стандартную функцию MS Excel «КОРРЕЛ» вычисляем значение линейного коэффициента корреляции для нашей задачи функция будет иметь вид «=КОРРЕЛ(B2:B16;C2:C16)», а значение rxy=0,96. Полученное значение коэффициента корреляции указывает на прямую и сильную связь наличия техники и объемов выращенной продукции.

Находим выборочный коэффициент линейной регрессии 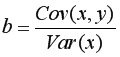=36,87; параметр 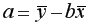=-17,78. Значит, уравнение парной линейной регрессии имеет вид 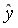=-17,78+36,87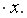

Коэффициент 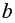 показывает, что при увеличении количества техники на 1 ед/га объем выращенной продукции  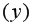в среднем увеличится на 36,875 тыс. ден. ед. (рис. 9.5)

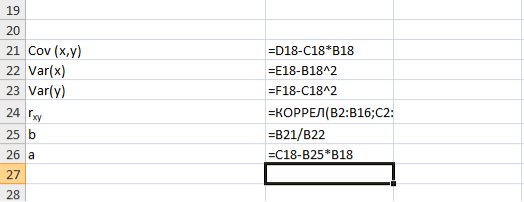
Рис. 9.5. Расчет параметров уравнения регрессии.

Таким образом, уравнение регрессии будет иметь вид: .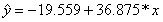

Подставляем в полученное уравнение фактические значения x (количество техники) находим теоретические значения объемов выращенной продукции (рис. 9.6).

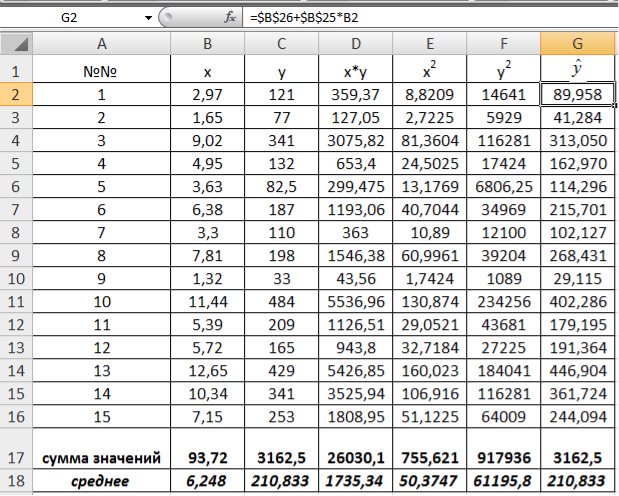
Рис. 9.6. Расчет теоретических значений объемов выращенной продукции

Используя Мастер диаграмм строим корреляционные поля (выделяя столбцы со значениями  и ) и уравнение линейной регрессии (выделяя столбцы со значениями  и 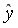). Выбираем тип диаграммы – Точечная В полученной диаграмме заполняем нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим график представленный на рис. 9.7.

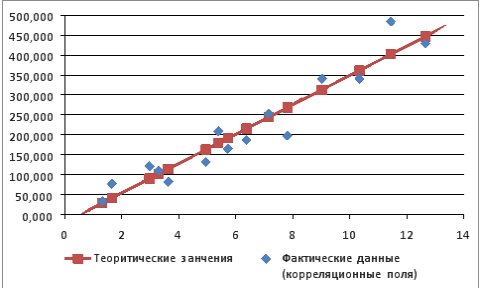
Рис. 9.7. График зависимости объема выращенной продукции от количества техники

Для оценки качества построенной модели регрессии вычислим:

• коэффициент детерминации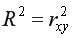=0,92, который показывает, что изменение затрат на выпуск продукции  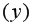на 92% объясняется изменением объема произведенной продукции  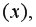а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;

• среднюю ошибку аппроксимации. Для этого в столбце H вычислим разность фактического и теоретического значений 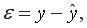 а в столбце I – выражение 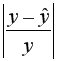. Обращаем Ваше внимание, что для вычисления значения по модулю используется стандартная функция MS Excel «ABS». При умножении среднего значения (ячейка I18) на 100% получим 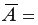18,2%. Следовательно, в среднем теоретические значения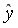отклоняются от фактических 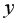на 18,2%(рис. 1.8).

С помощью 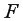-критерия Фишераоценим значимость уравнения регрессии в целом: 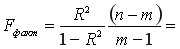150,74.

На уровне значимости 0,05 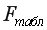=4,67 определяем c помощью встроенной статистической функции FРАСПОБР (рис. 1.9). При этом необходимо помнить, что «Степени_свободы1» это знаменатель 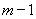, а «Степени_свободы2» – числитель 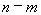, где 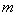 – число параметров в уравнении регрессии (у нас 2), n – число исходных пар значений (у нас 15).

Так как 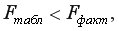 то уравнение регрессии значимо при 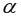=0,05.

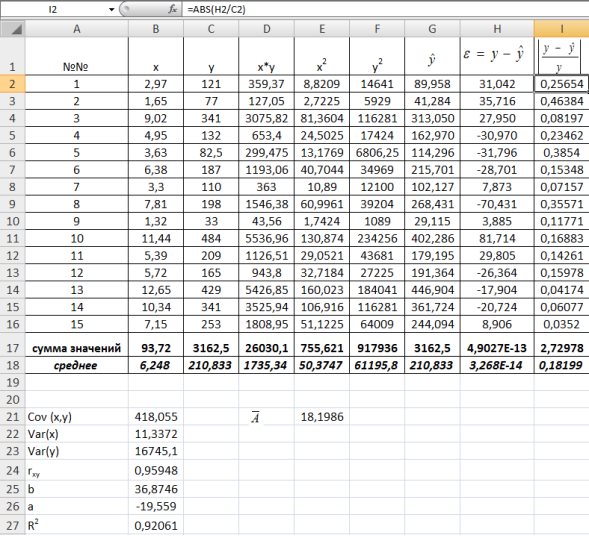
Рис. 9.8. Определение коэффициента детерминации и средней ошибки апроксимации

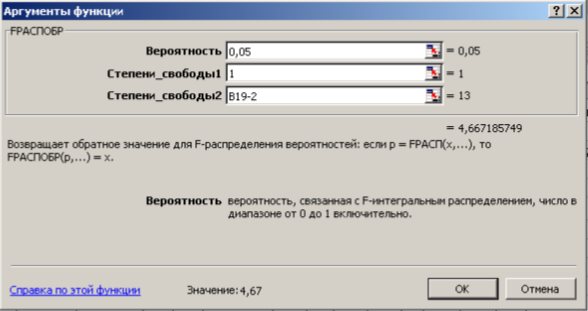
Рис. 9.9. Диалоговое окно функции FРАСПОБР

Далее определяем средний коэффициент эластичности по формуле. 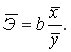Найденное 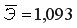показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1,093%.

Рассчитаем прогнозное значение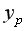путем подстановки в уравнение регрессии 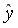=-19,559+36,8746 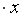прогнозного значения фактора 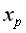=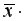1,12=6,248*1,12=6,9978. Получим 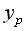=238,48. Следовательно, при количестве техники в количестве 6,9978ед/гаобъем выпущенной продукции составит 238,48 тыс. ден. ед.

Найдем остаточную дисперсию, для этого вычислим сумму квадратов разности фактического и теоретического значений. 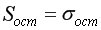=39,166 поместив следующую формулу =КОРЕНЬ(J17/(B19-2))в ячейку H21 (рис. 9.10).

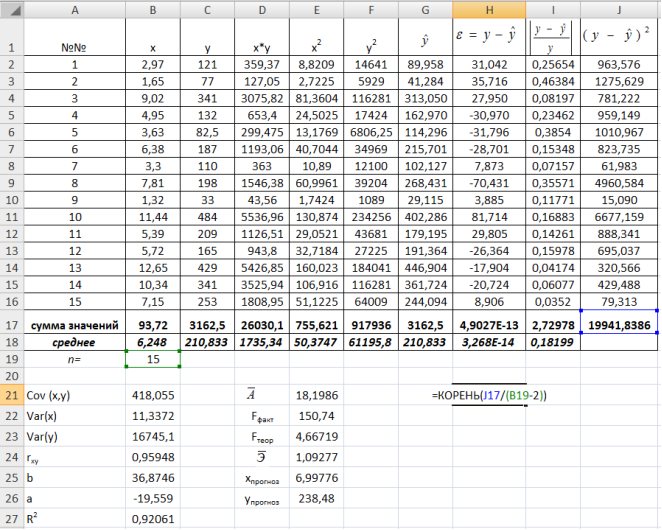
Рис. 9.10. Определение остаточной дисперсии

Средняя стандартная ошибка прогноза:

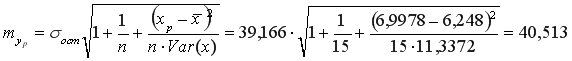
На уровне значимости 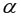=0,05 с помощью встроенной статистической функции СТЬЮДРАСПОБР определим 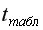=2,1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать .

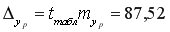Доверительный интервал прогноза:

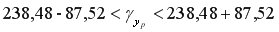 или .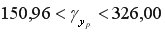

Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 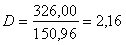 раза. Это произошло за счет малого объема наблюдений.

Необходимо отменить, что в MS Excel встроены статистические функции позволяющие значительно снизить количество промежуточных вычислений, например (рис. 9.11.):

Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.

Выборочная ковариация между 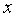 и 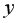 находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.

Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).

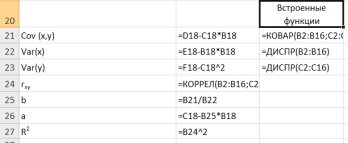
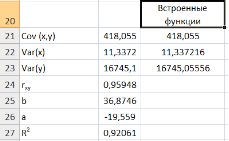
Рис.9.11. Вычисление показателей встроенными функциями MSExcel

Параметры линейной регрессии 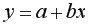 в Excel можно определить несколькими способами.

1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:

1. Выделить область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 – для получения только коэффициентов регрессии.

2. С помощью Мастера функций  среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 9.12):

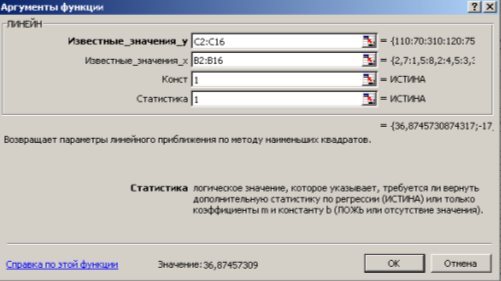
Рис. 9.12. Диалоговое окно ввода аргументов функции ЛИНЕЙН

Известные_значения_y – диапазон, содержащий данные результативного признака Y;

Известные_значения_x – диапазон, содержащий данные объясняющего признака X;

Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;

Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.

3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+ <SHIFT>+ <ENTER>.

Дополнительная регрессионная статистика будет выведена в виде (табл. 9.3):

Таблица 9.3

В результате применения функции ЛИНЕЙН получим:

(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:

1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню (через кнопку Microsoft Office получить доступ к параметрам MS Excel) в диалоговом окне «Параметры MSExcel» выбрать команду «Надстройки» и справа выбрать надстройку Пакета анализа далее нажать кнопку «Перейти» (рис. 9.13). В открывшемся диалоговом окне поставить галочку напротив «Пакет анализа» и нажать «ОК» (рис. 9.14).

На вкладке «Данные» в группе «Анализ» появится доступ к установленной надстройке. (рис. 9.15).

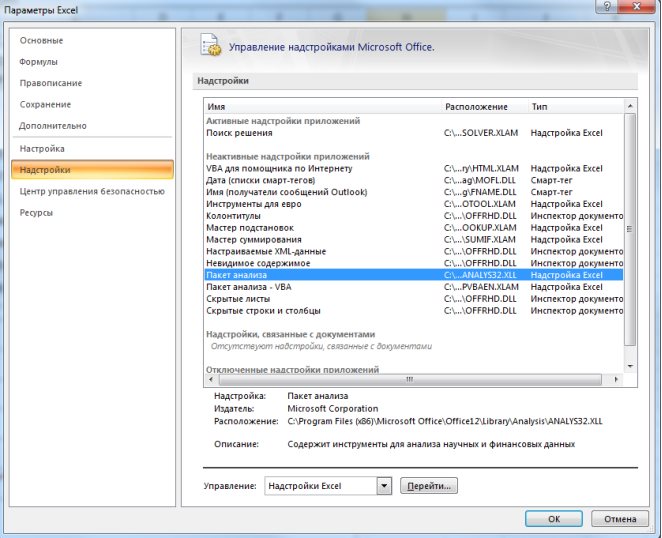
Рис. 9.13. Включение надстроек в MSExcel

Рис. 9.14. Диалоговое окно «Надстройки»

Рис. 9.15. Надстройка «Анализ данных» на ленте MSExcel 2007.

2. Выбрать на «Данные» в группе «Анализ» выбираем команду Анализ данных в открывшемся диалоговом окне выбрать инструмент анализа «Регрессия» и нажать «ОК» (рис. 9.16):

Рис. 9.16. Диалоговое окно «Анализ данных»

В появившемся диалоговом окне (рис. 9.17) заполнить поля:

Входной интервалY – диапазон, содержащий данные результативного признака Y;

Входной интервалX– диапазон, содержащий данные объясняющего признака X;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.

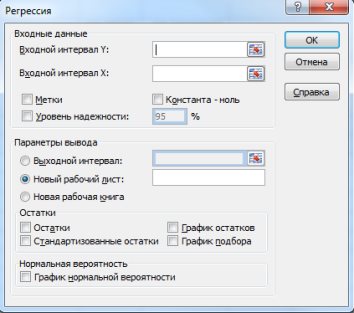
Рис. 9.17. Диалоговое окно «Регрессия»

Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне.

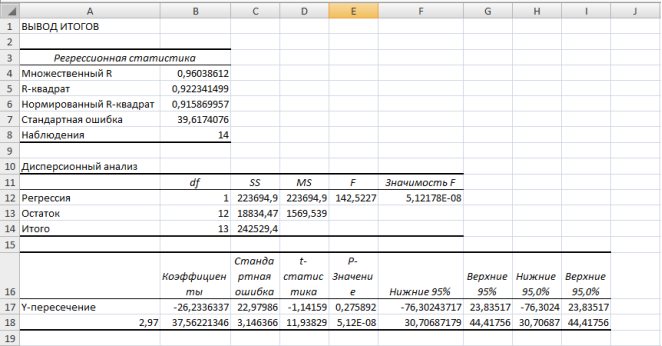
Рис. 9.18. Результаты применения инструмента Регрессия

В MSExcel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1. Необходимо выделить область построения диаграммы и в ленте выбрать «Макет» и в группе анализ выбрать команду «Линия тренда» (рис. 9.19.). В выпадающем пункте меню выбрать «Дополнительные параметры линии тренда».

Рис. 1.19. Лента

2. В появившемся диалоговом окне выбрать фактические значения, затем откроется диалоговое окно «Формат линии тренда» (рис. 9.20.) в котором выбирается вид линии тренда и устанавливаются соответствующие параметры.

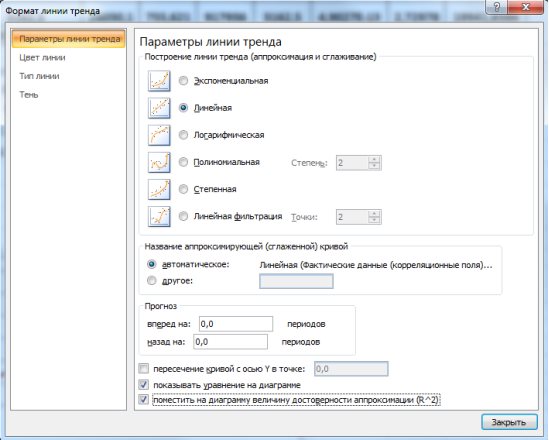
Рис. 9.20. Диалоговое окно «Формат линии тренда»

Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.

Выбираем Линейная для построения уравнения линейной регрессии.

В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину (рис.9.21).

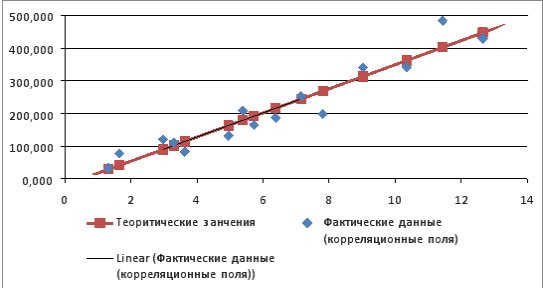
Рис. 9.21. Линейный тренд

Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 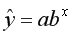 с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.