Пример 1. Вычислить предел: 
Решение: Числитель и знаменатель дроби, находящейся под знаком предела, стремятся к бесконечности (неопределенность типа  ). Для раскрытия этой неопределенности числитель и знаменатель дроби делим почленно на наивысшую степень переменной х в данном выражении, т.е. на
). Для раскрытия этой неопределенности числитель и знаменатель дроби делим почленно на наивысшую степень переменной х в данном выражении, т.е. на  .
.

так как  – бесконечно малые величины, при
– бесконечно малые величины, при  .
.
Пример 2. Вычислить предел: 
Решение: Числитель знаменатель дроби, находящейся под знаком предела, стремятся к нулю, т.е. имеем неопределенность типа  . Для раскрытия этой неопределенности следует провести тождественные преобразования с целью выделения в числителе и знаменателя множителя (х-3), который обращает их в 0 при x → 0. Для этого числитель и знаменатель дроби умножим на выражение, сопряженное числителю -
. Для раскрытия этой неопределенности следует провести тождественные преобразования с целью выделения в числителе и знаменателя множителя (х-3), который обращает их в 0 при x → 0. Для этого числитель и знаменатель дроби умножим на выражение, сопряженное числителю -  (тем самым избавимся от иррациональности в числителе). В знаменателе разложим квадратный трёхчлен
(тем самым избавимся от иррациональности в числителе). В знаменателе разложим квадратный трёхчлен  , на множители:
, на множители:

Получим:

Пример 3. Вычислить: 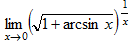
Решение: Имеем неопределенность типа 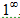 Преобразуем данное выражение следующим образом:
Преобразуем данное выражение следующим образом: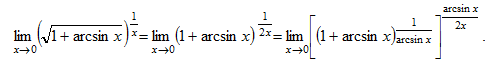
Вспомним что,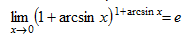 (второй замечательный предел), а
(второй замечательный предел), а 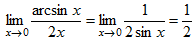 (первый замечательный предел).
(первый замечательный предел).
При решении применили метод замены переменной: t = arcsin х, тогда x = sin t.
Окончательно, получаем: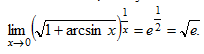
Пример 4. Найти частные производные первого порядка функции: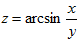
Решение:
Дифференцируем функцию сначала по х, считая у постоянной, а затем по у, считая х постоянной: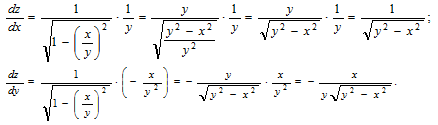
Пример 5. Задана функция полезности 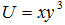 , где х и у – некоторые блага.
, где х и у – некоторые блага.
1) Найти, в каком направлении функция полезности воз-растает в точке (2;1) быстрее всего.
2) Найти наибольшую скорость возрастания функции полезности в точке (2;1).
Решение.
1) Функция полезности 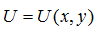 (скалярная функция) растет быстрее всего в направлении
(скалярная функция) растет быстрее всего в направлении 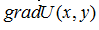 . Найдем частные производные
. Найдем частные производные 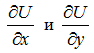 в точке (2;1):
в точке (2;1):
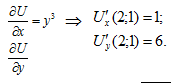
Таким образом, 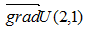 имеет координаты 1 и 6, т.е.
имеет координаты 1 и 6, т.е. 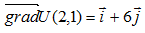 . Следовательно, функция
. Следовательно, функция 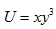 в точке (2;1) растет быстрее всего в направлении вектора
в точке (2;1) растет быстрее всего в направлении вектора 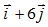 .
.
2) Скорость наибольшего возрастания функции 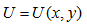 в точке (2;1) равна модулю
в точке (2;1) равна модулю 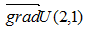 , т.е.
, т.е. 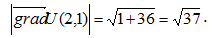
Написать комментарий
Ваше имя:Ваш комментарий:
Введите код, указанный на картинке:

